It is the fourth figure of a seven-step construction, which we will now carry out, step-by-step.

We will begin with any right triangle. The construction is easier to follow in case the triangle has all sides unequal, but any right triangle will do. The one shown here is the 3-4-5 triangle featured in the Chinese figure above.

Next we make three identical copies of the chosen right triangle. With these four identical right triangles, we intend to build a square, within the pink shadow.
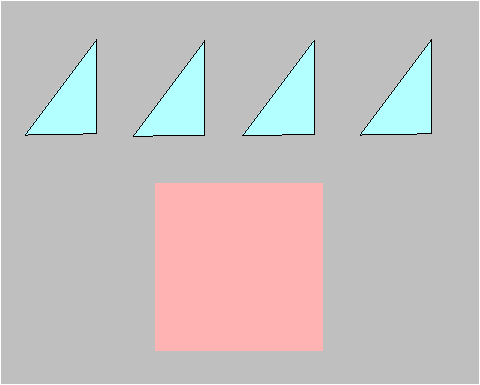
Step 1. Now we move the first of the four identical triangles down, so that its hypotenuse (the longest side) becomes the first side of a square.
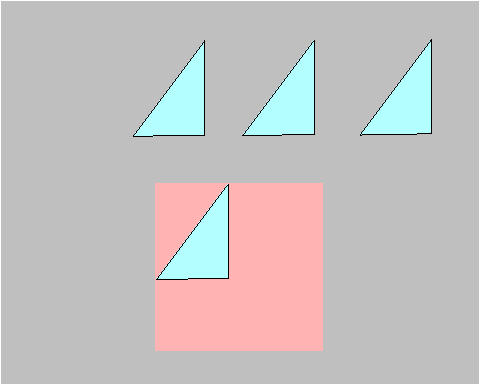
Step 2. Now, move the second triangle down, while rotating 90 degrees counterclockwise, to form the second side of the square we are constructing.
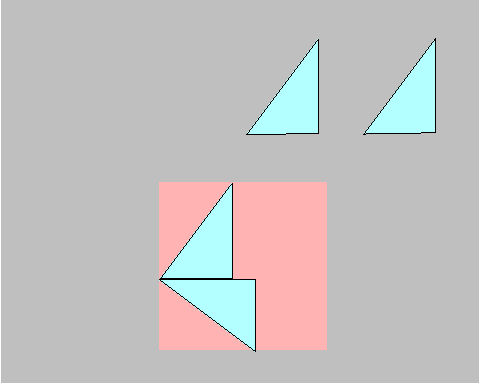
Step 3. Again, move the third triangle down, while rotating 180 degrees counterclockwise, to form the third side of the square we are constructing.
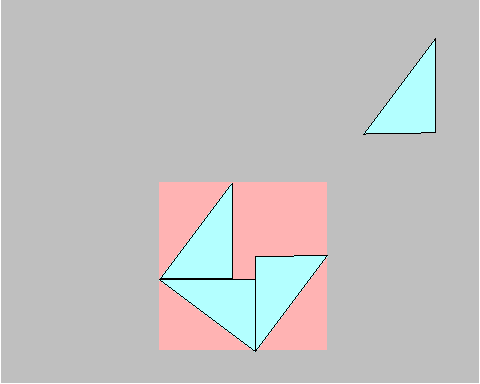
Step 4. Now, move the fourth triangle down, while rotating 270 degrees counterclockwise, to form the fourth side of the square we are constructing. This is the hsuang-thu.
NOTE that we have filled in the void in the center with a small yellow square. The four blue triangles plus the yellow square exactly cover the inclined "square on the hypotenuse".
NOTE ALSO that the remaining red portions of the original large red square could be covered by four more copies of the original triangle.

Now, with two more moves, we will transform square on the hypotenuse (the large light blue and yellow square) into two smaller squares.
Step 5. Move the fourth triangle again, rotating 90 degrees counterclockwise, underneath the third triangle.

Step 6. And now, move the first triangle again, rotating 90 degrees
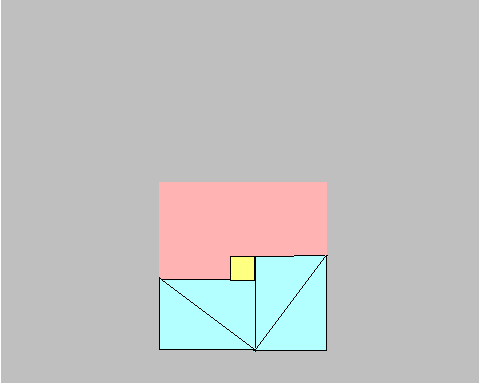
Et voila! See that the side of the medium size square outlined on the right is the medium side of the original triangle, while the side of the smaller square outlined on the left is the shorter side of the original triangle.
