Proposition 1.
On a given finite straight line to construct an equilateral triangle.
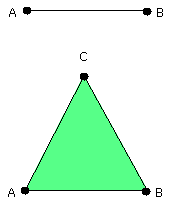Let AB be the given finite straight line.
Thus it is required to construct an equilateral triangle on the straight line AB.
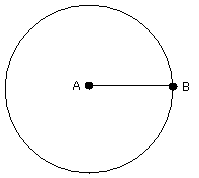With centre A and distance AB let the circle BCD be described
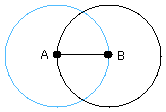again, with centre B and distance BA let the circle ACE be described
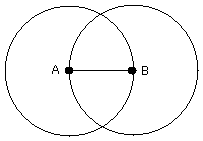and from the point C, in which the circles cut one another,
to the points A, B let the straight lines CA, CB be joined
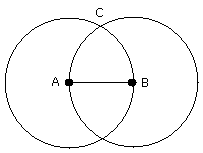Now, since the point A is the centre of the circle CDB,
AC is equal to AB.
Again, since the point B is the centre of the circle CAE,
BC is equal to BA.
But CA was also proved equal to AB; therefore each of the straight
lines CA, CB is eqaul to AB.
And things which are equal to the same thing are also equal to
one another, therefore CA is also equal to CB.
Therefore the three straight lines CA, AB, BC are equal to one another.
Therefore the triangle ABC is equilateral, and it has
been constructed on the given finite straight line AB.
(Being) what it was required to do.
Q.E.D
Ralph H. Abraham, 28 April, 1996.