Proposition 3.
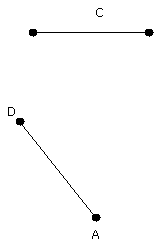
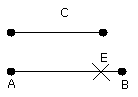 Let AB, C be the two unequal straight lines, and
let AB be the greater of them.
Thus it is required to cut off from AB the greater a
straight line equal to C the less.
Let AB, C be the two unequal straight lines, and
let AB be the greater of them.
Thus it is required to cut off from AB the greater a
straight line equal to C the less.
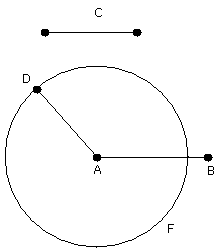 At the point A let AD be placed equal to the
straight line C
At the point A let AD be placed equal to the
straight line C
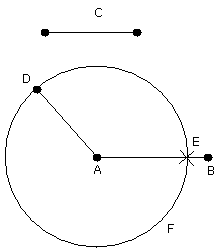 and with centre A and distance AD let the circle
DEF be described
and with centre A and distance AD let the circle
DEF be described
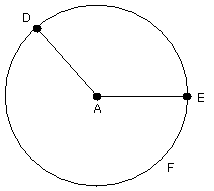 Now, since the point A is the centre of the circle DEF,
AE is equal to AD.
Now, since the point A is the centre of the circle DEF,
AE is equal to AD.
 But C is also equal to AD.
But C is also equal to AD.
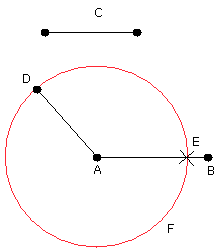 Therefore each of the straight lines AE, C is equal to AD; so that AE is also equal to C.
Therefore, given the two straight lines AB, C,
from AB the greater AE has been cut off equal to C the less.
(Being) what it was required to do.
Therefore each of the straight lines AE, C is equal to AD; so that AE is also equal to C.
Therefore, given the two straight lines AB, C,
from AB the greater AE has been cut off equal to C the less.
(Being) what it was required to do.
Q.E.F
Ralph H. Abraham, 28 April, 1996.
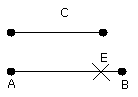 Let AB, C be the two unequal straight lines, and
let AB be the greater of them.
Thus it is required to cut off from AB the greater a
straight line equal to C the less.
Let AB, C be the two unequal straight lines, and
let AB be the greater of them.
Thus it is required to cut off from AB the greater a
straight line equal to C the less.
 At the point A let AD be placed equal to the
straight line C
At the point A let AD be placed equal to the
straight line C
 and with centre A and distance AD let the circle
DEF be described
and with centre A and distance AD let the circle
DEF be described
 Now, since the point A is the centre of the circle DEF,
AE is equal to AD.
Now, since the point A is the centre of the circle DEF,
AE is equal to AD.
 But C is also equal to AD.
But C is also equal to AD.
 Therefore each of the straight lines AE, C is equal to AD; so that AE is also equal to C.
Therefore, given the two straight lines AB, C,
from AB the greater AE has been cut off equal to C the less.
(Being) what it was required to do.
Therefore each of the straight lines AE, C is equal to AD; so that AE is also equal to C.
Therefore, given the two straight lines AB, C,
from AB the greater AE has been cut off equal to C the less.
(Being) what it was required to do.