If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, then they will also have the angles equal which are contained by the equal straight lines.
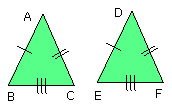Let ABC, DEF by two triangles having the two sides AB, AC
equal to the two sides DE, DF respectively, namely AB to DE,
and AC to DF; and let them have the base BC equal to the base EF;
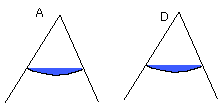I say that the angle BAC is also equal to the angle EDF.
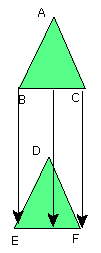For, if the triangle ABC be applied to the triangle DEF,
and if the point B be placed on the point E and the straight
line BC on EF,
the point C will also coincide with F,
because BC is equal to EF.
Then, BC coinciding with EF,
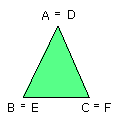BA, AC will also coincide with ED, DF
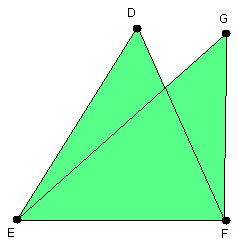For, if the base BC coincides with the base EF, and the
sides BA, AC do not coincide with ED, DF but fall beside
them as EG, GF,
then, given two straight lines constructed on a straight line
(from its extremities) and meeting in a point, there will
have been constructed on the same straight line (from its extremities),
and on the same side of it, two other straight lines meeting in
another point and equal to the former two respectively, namely
each to that which has the same extremity with it.
But they cannot be so constructed.
Therefore it is not possible that, if the base BC be applied
to the base EF, the sides BA, AC should not coincide with
ED, DF;
they will therefore coincide,
so that the angle BAC will also coincide with the angle
EDF, and will be equal to it.
Therefore etc.
Q.E.D