To bisect a given rectilineal angle.
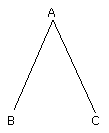Let the angle BAC be the given rectilineal angle.
Thus it is required to bisect it.
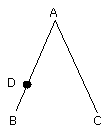Let a point D be taken at random on AB
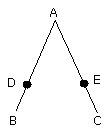let AE be cut off from AC equal to AD;
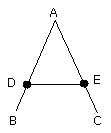Let DE be joined,
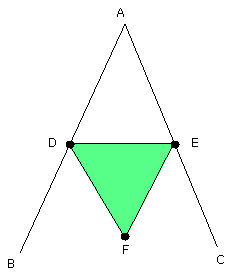and on DE let the equilateral triangle DEF be constructed;
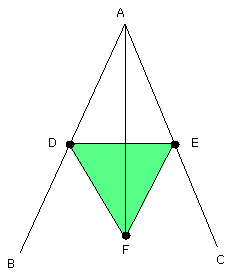let AF be joined.
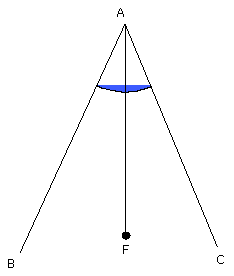I say that the angle BAC has been bisected by the straight line AF.
For, since AD is equal to AE,
and AF is common,
the two sides DA, AF are equal to the two sides EA, AF respectively.
And the base DF is equal to the base EF
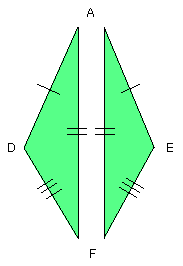therefore the angle DAF is equal to the angle EAF.
Therefore the given rectilineal angle BAC has been bisected by the
straight line AF.
Q.E.D
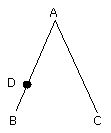As this is a construction, and within it two other constructions
are recalled (subroutines called), we may recall them, interpolate,
and show all the steps
Choose D.
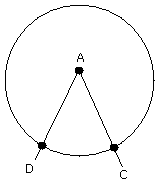With center A and distance AD draw a circle
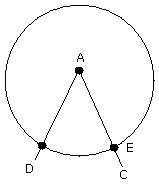Let E be the point where this circle cuts AC.
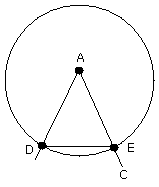Join DE
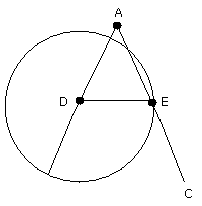With center D and distance DE draw circle.
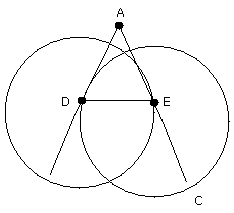With center E and distance DE draw circle.
Let F be the point of intersection of the two circles farther from A.
Join AF
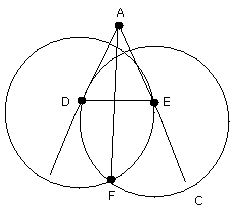Show all circles..