To draw a straight line at right angles to a given straight line from a given point on it.
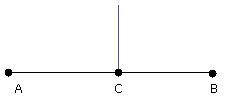Let AB be the given straight line, and C the given point on it.
Thus it is required to draw from the point C a straight line
at right angles to the straight line AB.
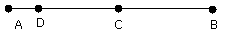Let a point D be taken at random on AC;
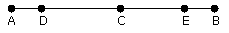let CE be made equal to CD;
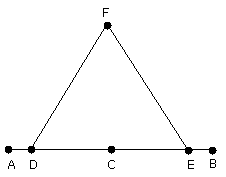on DE let the equilateral triangle FDE be constructed,
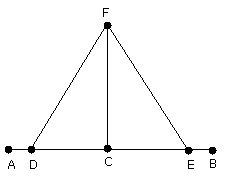and let FC be joined;
I say that the straight line FC has been drawn at right angles
to the given straight line AB from C the given point on it..
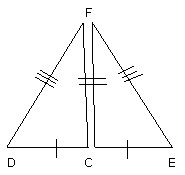For, since DC is equal to CE,
and CF is common,
the two sides DC, CF are equal to the two sides EC, CF respectively;
and the base DF is equal to the base FE
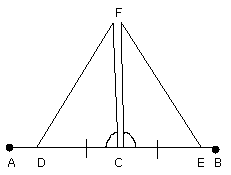therefore the angle DCF is equal to the angle ECF;
and they are adjacent angles.
But when a straight line set up on a straight line makes the
adjacent angles equal to one another, each of the equal
angles is right.
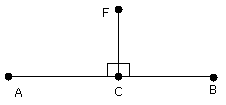
therefore each of the angles DCF, FCE is right.
Therefore the straight line CF has been drawn at right angles to the
given straight line AB from the given point C on it.
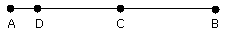Q.E.D
The 3 step construction may be unpacked as usual.
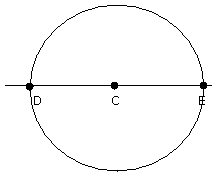Draw circle.
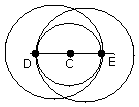Draw 2 circles
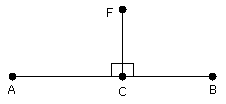Choose F as upper intersection. Join FC.