In any triangle, if one of the sides be produced, the exterior angle is equal to the two interior and opposite angles, and the three interior angles of the triangle are equal to two right angles.
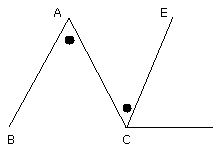
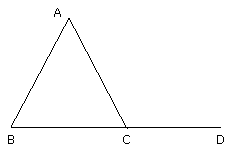Let ABC be a triangle, and let one side of it BC be produced to D;
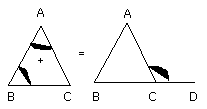I say that the exterior angle ACD is equal to the two interior and
opposite angles CAB, ABC, and the three interior angles of the triangle
ABC, BCA, CAB are equal to two right angles.
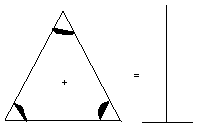
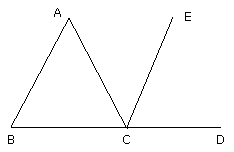For, let CE be drawn through the point C parallel to the straight line AB.
Then, since AB is parallel to CE, and AC has fallen upon them, the alternate
angles BAC, ACE are equal to one another.
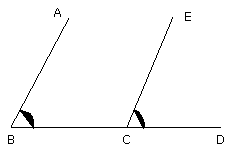Again, since AB is parallel to CE, and the straight line BD has fallen upon
them, the exterior angle ECD is equal to the interior and opposite angle ABC.
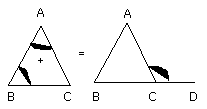But the angle ACE was also proved equal to the angle BAC;
therefore the whole angle ACD is equal to the two interior and opposite angles
BAC, ABC.
Let the angle ABC be added to each;
therefore the angles ACD, ACB are equal to the three angles ABC, BCA, CAB.
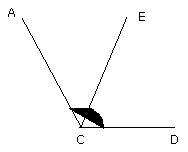
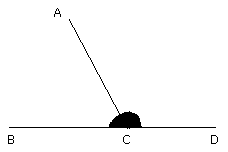
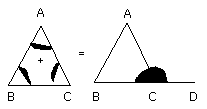But the angles ACD, ACB are equal to two right angles;
therefore the angles ABC, BCA, CAB are also equal to two right angles.
Therefore etc.
Q.E.D