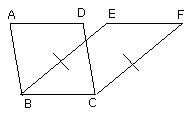
Parallelograms which are on the same base and in the same parallels are equal to one another.
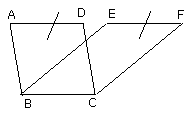
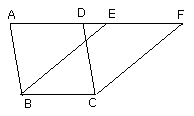Let ABCD, EBCF be parallelograms on the same base BC and in the same
parallels AF, BC;
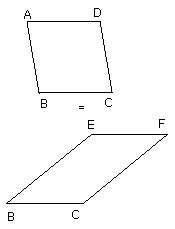I say that ABCD is equal to the parallelogram EBCF
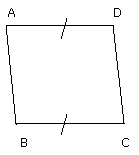For, since ABCD is a parallelogram, AD is equal to BC.
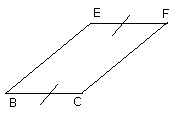EF is equal to BC,
so that AD is also equal to EF;
and DE is common;
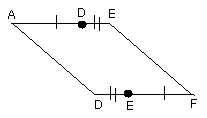therefore the whole AE is equal to the whole DF.
But AB is also equal to DC;
therefore the two sides EA, AB are equal to the two sides FD, DC respectively,
and the angle FDC is equal to the angle EAB, the exterior to the interior;
therefore the base EB is equal to the base FC
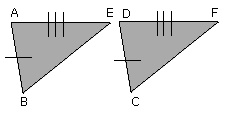
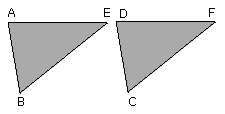and the triangle EAB will be equal to the triangle FDC.
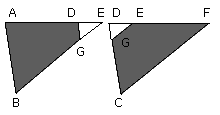let DGE be subtracted from each;
therefore the The trapezium ABGD which remains is equal to the trapezium
EGCF which remains.
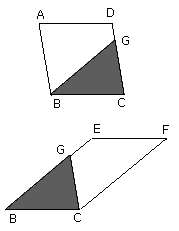Let the triangle GBC be added to each.;
Therefore the whole parallelogram ABCD is equal to the whole parallelogram ECBF.
Therefore etc.
Q.E.D