To a given straight line to apply, in a given rectilineal angle, a parallelogram equal to a given triangle.
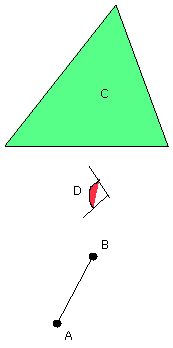Let AB be the given straight line, C the given triangle and D the given
rectilineal angle;
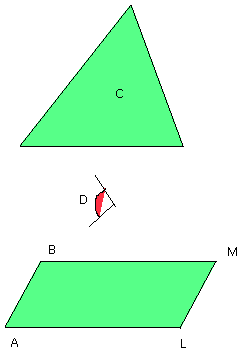thus it is required to apply to the given straight line AB, in the angle equal
to the angle D, a parallelogram equal to the given triangle C.
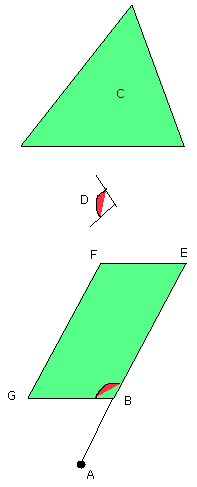Let the parallelogram BEFG be constructed equal to the triangle C, in the
angle EBG which is equal to D; let it be placed so that BE is in a straight
line with AB;
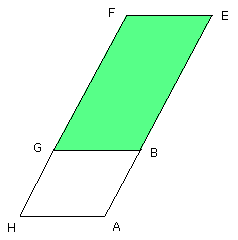let FG be drawn through to H, and let AH be drawn through A parallel to BG
or EF.
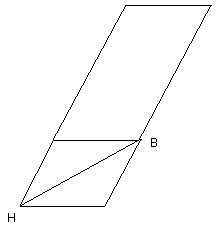Let HB be joined.
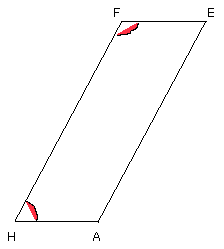Then, since the straight line HF falls upon the parallels AH, EF,
the angles AHF, HFE are equal to two right angles.
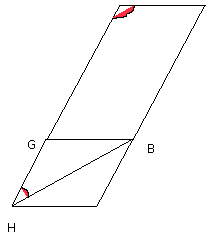Therefore the angles BHG, GFE are less than two right angles;
and straight lines produced indefinitely from angles less thatn two right
angles meet;
therefore HB, FE, when produced, will meet.
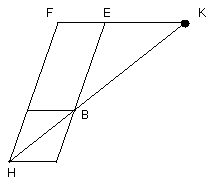Let them be produced and meet at K;
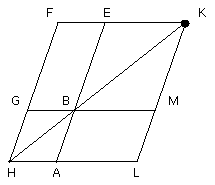through the point K let KL be drawn parallel to either EA or FH, and let HA,
GB be produced to the points L, M.
Then HLKF is a parallelogram, KH is its diameter, and AG, ME are
parallelograms, and LB, BF the so-called complements, about HK;
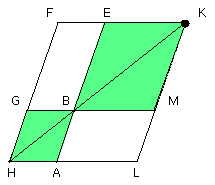
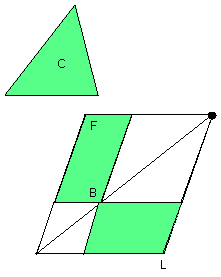therefore LB is equal to BF.
But BF is equal to the triangle C;
therefore LB is also equal to C.
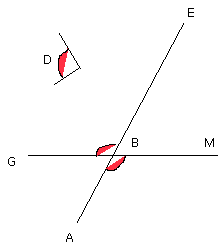And, since the angle GBE is equal to the angle ABM,
while the angle GBE is equal to D.
Therefore the parallelogram LB equal to the given triangle C has been applied
to the given straight line AB, in the angle ABM which is equal to D.
Q.E.F