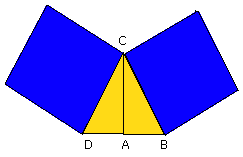
If in a triangle the square on one of the sides be equal to the squares on the remaining two sides of the triangle, the angle contained by the remaining two sides of the triangle is right.
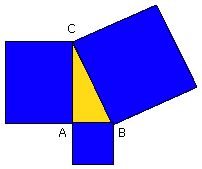For in the triangle ABC let the square on one side BC be equal to the squares
on the sides BA, AC.
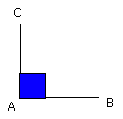I say that the angle BAC is right.
Proof
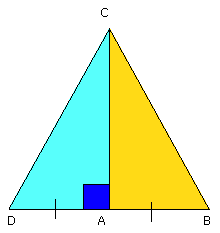
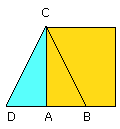
For let AD be drawn from the point A at right angles to the straight line AC,
let AD be make equal to BA, and let DC be joined.
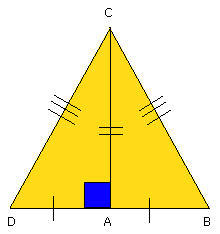
Since DA is equal to AB, the square on DA is also equal to the square on AB.
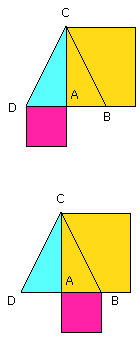
Let the square on AC be added to each; therefore the squares on DA, AC are
equal to the squares on BA, AC.
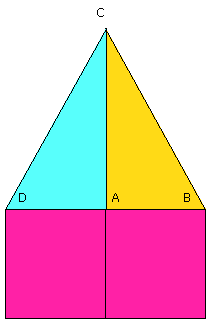
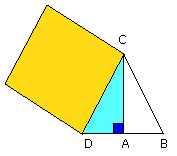But the square on DC is equal to the squares on DA, AC, for the angle DAC is
right;
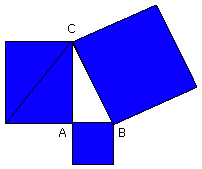and the square on BC is equal to the squares on BA, AC, for this is the
hypothesis;
therefore the square on DC is equal to the square on BC.
so that the side DC is also equal to BC.
And, since DA is equal to AB, and AC is common, the two sides DA, AC are
equal to the two sides BA, AC;
and the base DC is equal to the base BC;
therefore the angle DAC is equal to the angle BAC.
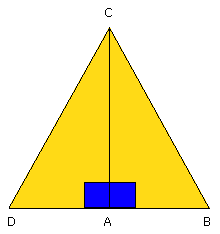But the angle DAC is right;
therefore the angle BAC is also right.
Therefore etc.
Q.E.D