To cut a given straight line so that the rectangle contained by the whole and one of the segments is equal to the square on the remaining segment.
Let AB be the given straight line;
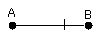thus it is required to cut AB
so that the rectangle contained by the whole and one of the segments
is equal to the square on the remaining segment.
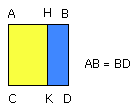
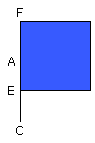
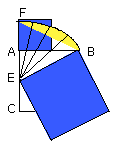
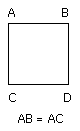For let the square ABDC be described on AB;
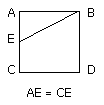let AC be bisected at the point E, and let BE be joined;
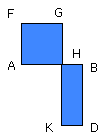
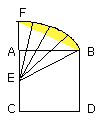let CA be drawn through to F, and let EF be made equal to BE;
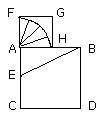let the square FH be described on AF, and
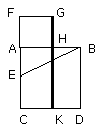let GH be drawn through to K.
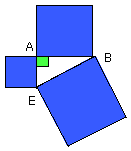
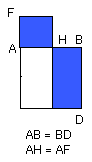I say that AB has been cut at H so as to make the rectangle contained by AB,
BH equal to the square on AH.
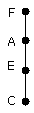For, since the straight line AC has been bisected at E, and FA is added to it,
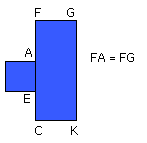the rectangle contained by CF, FA together with the square on AE
is equal to the square on EF
But EF is equal to EB; therefore the rectangle CF, FA together with the square
on AE is equal to the square on EB.
But the squares on BA, AE are equal to the square on EB, for the angle at A is
right;
therefore the rectangle CF, FA together with the square on AE is equal to the
squares on BA, AE.
Let the square on AE be subtracted from each; therefore the rectangle CF, FA
which remains is equal to the square on AB.
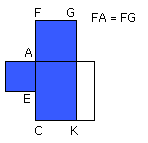
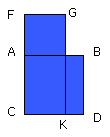Now the rectangle CF, FA is FK, for AF is equal to FG; and the square on AB is
AD;
therefore FK is equal to AD.
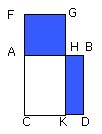Let AK be subtracted from each; therefore FH which remains is equal to HD.
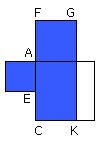
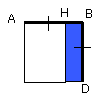And HD is the rectangle AB, BH, for AB is equal to BD;
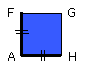and FH is the square on AH;
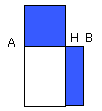therefore the rectangle contained by AB, BH is equal to the square on HA.
Therefore the given straight line AB has been cut at H so as to make the
rectangle contained by AB, BH equal to the square on HA.
Q.E.F.