If in a circle two straight lines cut one another which are not through the centre, they do not bisect one another.
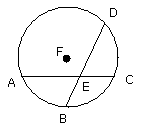
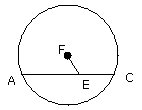
Let ABCD be a circle, and in it let the two straight lines AC, BD, which are
not through the centre, cut one another at E; I say that they do not bisect
one another.
For, if possible, let them bisect one another, so that AE is equal to EC, and
BE to ED;
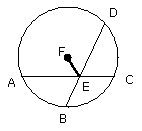let the centre of the circle ABCD be taken, and let it be F; let FE be joined.
Then, since a straight line FE through the centre bisects a straight line AC
not through the centre,
it also cuts it at right angles; therefore the angle FEA is right.
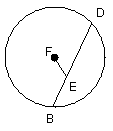Again, since a straight line FE bisects a straight line BD,
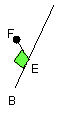t also cuts it at right angles [III. 3]; therefore the angle FEB is right.
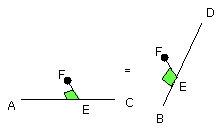But the angle FEA was also proved right; therefore the angle FEA is equal to
the angle FEB, the less to the greater; which is impossible.
Therefore AC, BD do not bisect one another
Therefore, etc.
Q.E.D.