From a given point to draw a straight line touching a given circle.
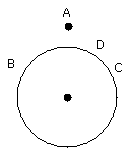Let A be the given point, and BCD the given circle; thus it is required to
draw from the point A a straight line touching the circle BCD.
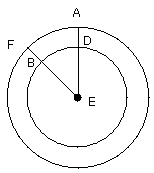
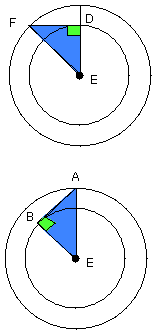
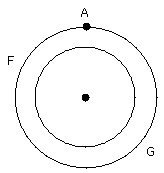For let the centre E of the circle be taken;
let AE be joined, and with centre E and distance EA let the circle AFG be
described;
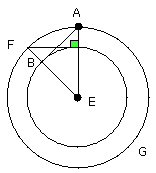from D let DF be drawn at right angles to EA, and let EF, AB be joined;
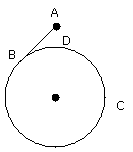I say that AB has been drawn from the point A touching the circle BCD.
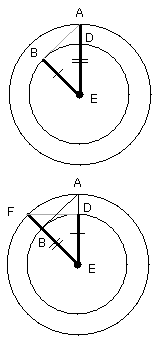
For, since E is the centre of the circles BCD, AFG, EA is equal to EF, and ED
to EB;
therefore the two sides AE, EB are equal to the two sides FE, ED:
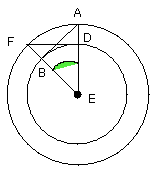and they contain a common angle, the angle at E;
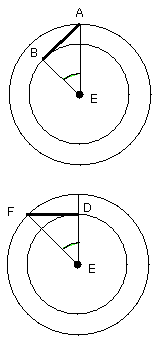therefore the base DF is equal to the base AB,
and the triangle DEF is equal to the triangle BEA, and the remaining angles to
the remaining angles; therefore the angle EDF is equal to the angle EBA.
But the angle EDF is right; therefore the angle EBA is also right.
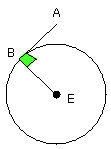Now EB is a radius; and the straight line drawn at right angles to the
diameter of a circle, from its extremity, touches the circle; therefore AB
touches the circle BCD.
Therefore from the given point A the straight line AB has been drawn touching
the circle BCD.