If a straight line touch a circle, and from the point of contact a straight line be drawn at right angles to the tangent, the center of the circle will be on the straight line so drawn.
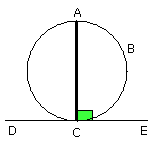 For let a straight line DE touch the circle ABC at the point C, and from C let
CA be drawn at right angles to DE; I say that the centre of the circle is on AC.
For let a straight line DE touch the circle ABC at the point C, and from C let
CA be drawn at right angles to DE; I say that the centre of the circle is on AC.
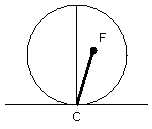 For suppose it is not, but, if possible, let F be the centre, and let CF be
joined.
For suppose it is not, but, if possible, let F be the centre, and let CF be
joined.
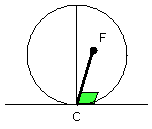 Since a straight line DE touches the circle ABC, and FC has been joined from
the centre to the point of contact, FC is perpendicular to DE; therefore the
angle FCE is right.
Since a straight line DE touches the circle ABC, and FC has been joined from
the centre to the point of contact, FC is perpendicular to DE; therefore the
angle FCE is right.
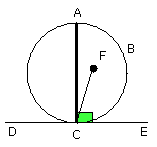 But the angle ACE is also right; therefore the angle FCE is equal to the angle
ACE, the less to the greater: which is impossible.
But the angle ACE is also right; therefore the angle FCE is equal to the angle
ACE, the less to the greater: which is impossible.
Therefore F is not the centre of the circle ABC.
Similarly we can prove that neither is any other point except a point on AC.
Therefore, etc.
Q.E.D.