On the same straight line there cannot be constructed two similar and unequal segments of circles on the same side.
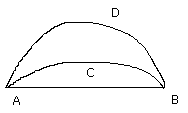For, if possible, on the same straight line AB let two similar and unequal
segments of circles ACB, ADB be constructed on the same side;
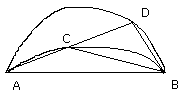et ACD be drawn through, and let CB, DB be joined.
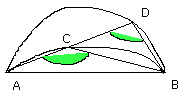Then, since the segment, ACB is similar to the segment ADB, and similar
segments of circles are those which admit equal angles, the angle ACB is equal
to the angle ADB, the exterior to the interior: which is impossible.
Therefore, etc.
Q.E.D.