In equal circles equal angles stand on equal circumferences, whether they stand at the centres or at the circumferences.
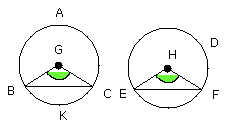Let ABC, DEF be equal circles, and in them let there be equal angles, namely
at the centres the angles BGC, EHF,
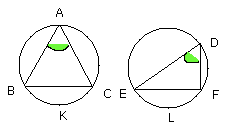and at the circumferences the angles BAC, EDF; I say that the circumference
BKC is equal to the circumference ELF.
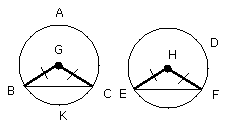For let BC, EF be joined.
Now, since the circles ABC, DEF are equal, the radii are equal.
Thus the two straight lines BG, GC are equal to the two straight lines EH, HF;
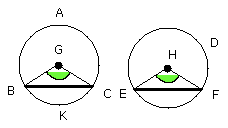and the angle at G is equal to the angle at H; therefore the base BC is equal
to the base EF [I. 4].
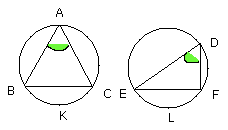And, since the angle at A is equal to the angle at D, the segment BAC is
similar to the segment EDF.
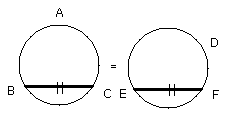and they are upon equal straight lines.
But similar segments of circles on equal straight lines are equal to one
another;
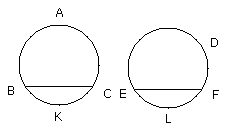therefore the segment BAC is equal to EDF. But the whole circle ABC is also
equal to the whole circle DEF; therefore
the circumference BKC which remains is equal to the circumference ELF.
Therefore, etc.
Q.E.D.