If a straight line touch a circle, and from the point of contact there be drawn across, in the circle, a straight line cutting the circle, the angles which it makes with the tangent will be equal to the angles in the alternate segments of the circle.
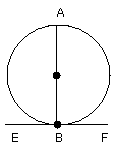
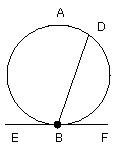For let a straight line EF touch the circle ABCD at the point B, and from the
point B let there be drawn across, in the circle ABCD, a straight line BD
cutting it;
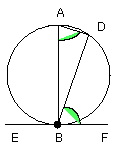I say that the angles which BD makes with the tangent EF will be equal to the
angles in the alternate segments of the circle, that is, that the angle FBD is
equal to the angle constructed in the segment BAD,
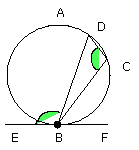and the angle EBD is equal to the angle constructed in the segment DCB.
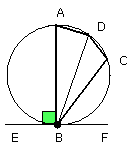For let BA be drawn from B at right angles to EF, let a point C be taken at
random on the circumference BD, and let AD, DC, CB be joined.
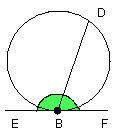
Then, since a straight line EF touches the circle ABCD at B, and BA has been
drawn from the point of contact at right angles to the tangent, the centre of
the circle ABCD is on BA.
Therefore BA is a diameter of the circle ABCD;
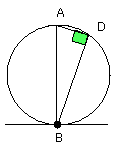therefore the angle ADB, being an angle in a semicircle, is right.
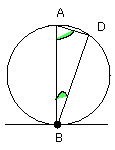Therefore the remaining angles BAD, ABD are equal to one right angle.
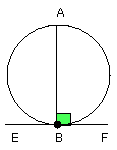But the angle ABF is also right; therefore the angle ABF is equal to the
angles BAD, ABD.
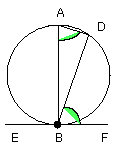Let the angle ABD be subtracted from each; therefore the angle DBF which
remains is equal to the angle BAD in the alternate segment of the circle.
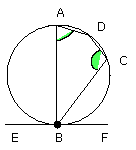Next, since ABCD is a quadrilateral in a circle, its opposite angles are equal
to two right angles.
But the angles DBF, DBE are also equal to two right angles;
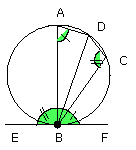therefore the angles DBF, DBE are equal to the angles BAD, BCD, of which the
angle BAD was proved equal to the angle DBF; therefore the angle BAD was
proved equal to the angle DBF; therefore the angle DBE which remains is equal
to the angle DCB in the alternate segment DCB of the circle.
Therefore, etc.
Q.E.D.