If a point be taken outside a circle and from it there fall on the circle two straight lines, and if one of them cut the circle and the other touch it, the rectangle contained by the whole of the straight line which cuts the circle and the straight line intercepted on it outside between the point and the convex circumference will be equal to the square on the tangent.
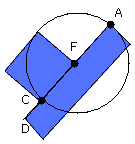
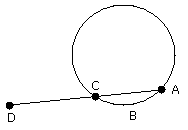
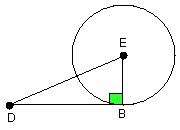
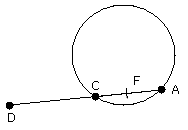
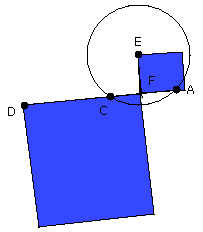
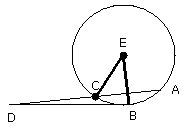
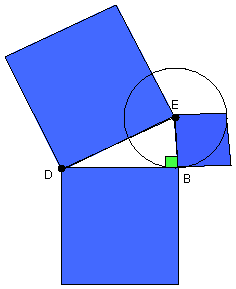
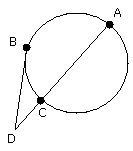 For let a point D be taken outside the circle ABC, and from D let the two
straight lines DCA, DB fall on the circle ABC; let DCA cut the circle ABC and
let BD touch it;
For let a point D be taken outside the circle ABC, and from D let the two
straight lines DCA, DB fall on the circle ABC; let DCA cut the circle ABC and
let BD touch it;
 I say that the rectangle contained by AD, DC is equal to the square on DB.
I say that the rectangle contained by AD, DC is equal to the square on DB.
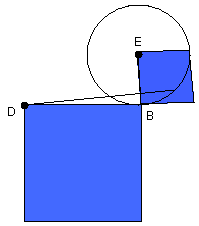
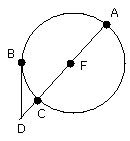 Then DCA is either through the centre or not through the centre.
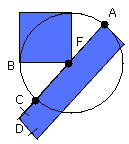
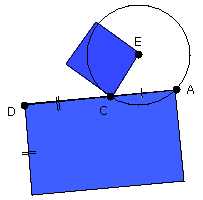
First let it be through the centre, and let F be the centre of the circle ABC;
Then DCA is either through the centre or not through the centre.
First let it be through the centre, and let F be the centre of the circle ABC;
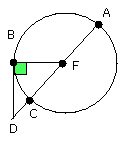 let FB be joined; therefore the angle FBD is right.
let FB be joined; therefore the angle FBD is right.
 And, since AC has been bisected at F, and CD is added to it, the rectangle AD,
DC together with the square on FC
And, since AC has been bisected at F, and CD is added to it, the rectangle AD,
DC together with the square on FC
 is equal to the square on FD.
is equal to the square on FD.
 But FC is equal to FB; therefore the rectangle AD, DC together with the square
on FB is equal to the square on FD.
But FC is equal to FB; therefore the rectangle AD, DC together with the square
on FB is equal to the square on FD.
 And the squares on FB, BD are equal to the square on FD;
And the squares on FB, BD are equal to the square on FD;
 therefore the rectangle AD, DC together with the square on FB
therefore the rectangle AD, DC together with the square on FB
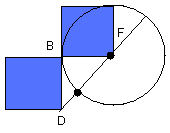 is equal to the squares on FB, BD.
is equal to the squares on FB, BD.
 Let the square on FB be subtracted from each; therefore the rectangle AD, DC
which remains is equal to the square on the tangent DB.
Let the square on FB be subtracted from each; therefore the rectangle AD, DC
which remains is equal to the square on the tangent DB.
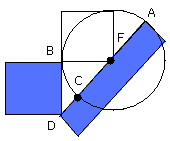
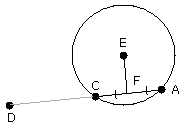
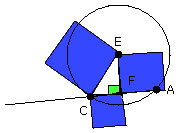
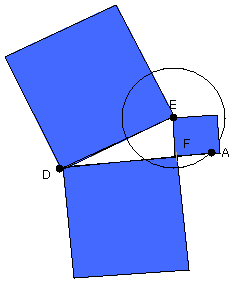
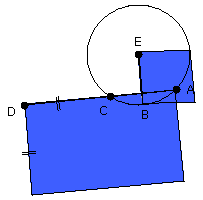
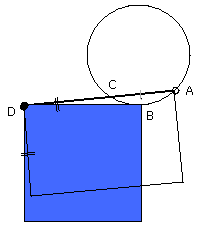
 Again, let DCA not be through the centre of the circle ABC;
Again, let DCA not be through the centre of the circle ABC;
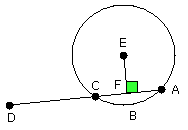 let the centre E be taken, and from E let EF be drawn perpendicular to AC;
let the centre E be taken, and from E let EF be drawn perpendicular to AC;
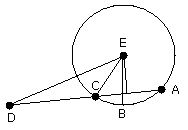 let EB, EC, ED be joined.
let EB, EC, ED be joined.
 Then the angle EBD is right.
Then the angle EBD is right.
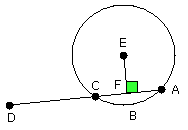 And, since a straight line EF through the centre cuts a straight line AC not
through the centre at right angles,
And, since a straight line EF through the centre cuts a straight line AC not
through the centre at right angles,
 it also bisects it [III. 3]; therefore AF is equal to FC.
it also bisects it [III. 3]; therefore AF is equal to FC.
 Now, since the straight line AC has been bisected at the point F, and CD is
added to it,
Now, since the straight line AC has been bisected at the point F, and CD is
added to it,
 the rectangle contained by AD, DC together with the square on FC
the rectangle contained by AD, DC together with the square on FC
is equal to the square on FD.
 Let the square on FE be added to each;
therefore the rectangle AD, DC together with the squares on DF, FE
Let the square on FE be added to each;
therefore the rectangle AD, DC together with the squares on DF, FE
 is equal to the squares on FD, FE.
is equal to the squares on FD, FE.
 But the square on EC is equal to the squares on CF, FE, for the angle EFC is
right;
But the square on EC is equal to the squares on CF, FE, for the angle EFC is
right;
 and the square on ED is equal to the squares on DF, FE;
and the square on ED is equal to the squares on DF, FE;
 therefore the rectangle AD, DC together with the square on EC
therefore the rectangle AD, DC together with the square on EC
 is equal to the square on ED.
is equal to the square on ED.
 And EC is equal to EB;
And EC is equal to EB;
 therefore the rectangle AD, DC together with the square on EB
therefore the rectangle AD, DC together with the square on EB
 is equal to the square on ED.
is equal to the square on ED.
 But the squares on EB, BD are equal to the square on ED, for the angle EBD is
right;
But the squares on EB, BD are equal to the square on ED, for the angle EBD is
right;
 and the square on ED is equal to the squares on DF, FE; therefore the
rectangle AD, DC together with the square on EB is equal to the square on ED.
But the squares on EB, BD are equal to the square on ED, for the angle ABD is
right [I. 47]; therefore the rectangle AD, DC together with the square on EB
is equal to the squares on EB, BD.
and the square on ED is equal to the squares on DF, FE; therefore the
rectangle AD, DC together with the square on EB is equal to the square on ED.
But the squares on EB, BD are equal to the square on ED, for the angle ABD is
right [I. 47]; therefore the rectangle AD, DC together with the square on EB
is equal to the squares on EB, BD.
 Let the square on EB be subtracted from each; therefore the rectangle AD, DC
which remains is equal to the square on DB.
Let the square on EB be subtracted from each; therefore the rectangle AD, DC
which remains is equal to the square on DB.
Therefore, etc;
Q.E.D.