In a given circle to inscribe a triangle equiangular with a given triangle.
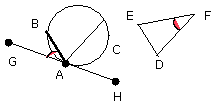
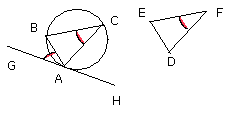
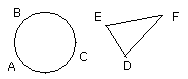 Let ABC be the given circle, and DEF the given triangle;
Let ABC be the given circle, and DEF the given triangle;
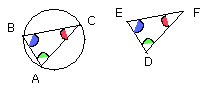 thus it is required to inscribe in the circle ABC a triangle equiangular with
the triangle DEF.
thus it is required to inscribe in the circle ABC a triangle equiangular with
the triangle DEF.
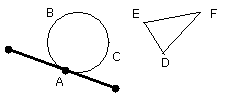 Let GH be drawn touching the circle ABC at A [III. 16, Por.];
Let GH be drawn touching the circle ABC at A [III. 16, Por.];
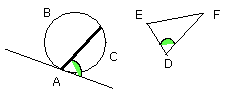 on the straight line AH, and at the point A on it, let the angle HAC be
constructed equal to the angle DEF,
on the straight line AH, and at the point A on it, let the angle HAC be
constructed equal to the angle DEF,
 and on the straight line AG, and at the point A on it, let the angle GAB be
constructed equal to the angle DFE [I. 23];
and on the straight line AG, and at the point A on it, let the angle GAB be
constructed equal to the angle DFE [I. 23];
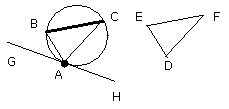 let BC be joined.
let BC be joined.
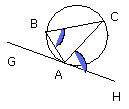 Then, since a straight line AH touches the circle ABC, and from the point of
contact at A the straight line AC is drawn across in the circle, therefore the
angle HAC is equal to the angle ABC in the alternate segment of the circle,
Then, since a straight line AH touches the circle ABC, and from the point of
contact at A the straight line AC is drawn across in the circle, therefore the
angle HAC is equal to the angle ABC in the alternate segment of the circle,
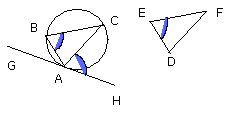 therefore the angle HAC is equal to the angle ABC in the alternate segment of
the circle [III. 32].
But the angle HAC is equal to the angle DEF; therefore the angle ABC is also
equal to the angle DEF.
therefore the angle HAC is equal to the angle ABC in the alternate segment of
the circle [III. 32].
But the angle HAC is equal to the angle DEF; therefore the angle ABC is also
equal to the angle DEF.
 For the same reason the angle ACB is also equal to the angle DFE;
For the same reason the angle ACB is also equal to the angle DFE;
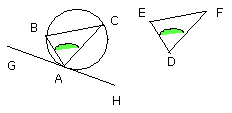 therefore the remaining angle BAC is also equal to the remaining angle EDF
[I. 32].
therefore the remaining angle BAC is also equal to the remaining angle EDF
[I. 32].
Therefore in the given circle there has been inscribed a triangle equiangular
with the given triangle.
Q.E.F.