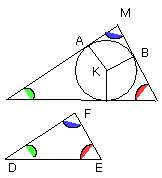
About a given circle to circumscribe a triangle equiangular with a given triangle.
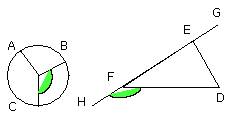
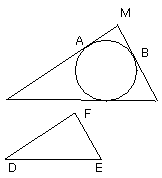Let ABC be the given circle, and DEF the given triangle; thus it is required
to circumscribe about the circle ABC a triangle equiangular with the triangle
DEF.
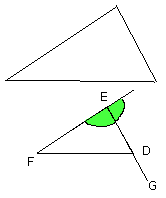
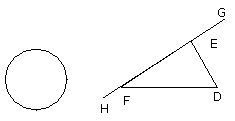Let EF be produced in both directions to the points G, H,
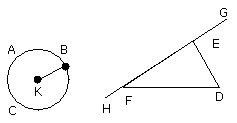let the centre K of the circle ABC be taken [III. 1], and let the straight
line KB be drawn across at random;
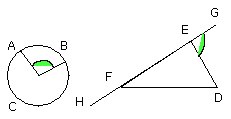on the straight line KB, and at the point K on it, let the angle BKA be
constructed equal to the angle DEG,
and the angle BKC equal to the angle DFH [I. 23];
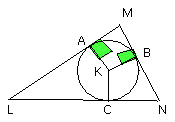
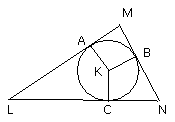and through the points A, B, C let LAM, MBN, NCL be drawn touching the circle
ABC [III. 16, Por.].
Now, since LM, MN, NL touch the circle ABC at the points A, B, C, and KA, KB,
KC have been joined from the centre K to the points A, B, C, therefore the
angles at the points A, B, C are right [III. 18].
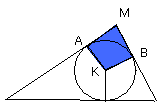And, since the four angles of the quadrilateral AMBK are equal to four right
angles, inasmuch as AMBK is in fact divisible into two triangles,
and the angles KAM, KBM are right,
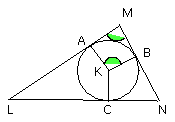therefore the remaining angles AKB, AMB are equal to two right angles.
But the angles DEG, DEF are also equal to two right angles [I. 13];
therefore the angles AKB, AMB are equal to the angles DEG, DEF,
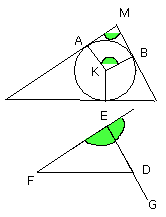
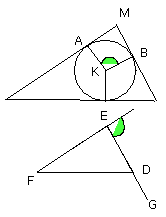of which the angle AKB is equal to the angle DEF;
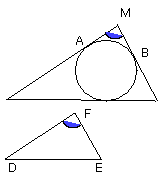therefore the angle AMB which remains
is equal to the angle DEF which remains
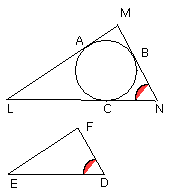Similarly it can be proved that the angle LNB is also equal to the angle DFE;
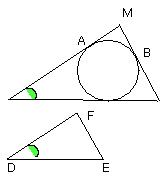therefore the remaining angle MLN is equal to the angle EDF [I. 32].
Therefore the triangle LMN is equiangular with the triangle DEF; and it has
been circumscribed about the circle ABC.
Therefore about a given circle there has been circumscribed a triangle
equiangular with the given triangle.
Q.E.F.