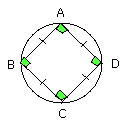
In a given circle to inscribe a square.
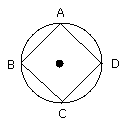 Let ABCD be the given circle; thus it is required to inscribe a square in the
circle ABCD.
Let ABCD be the given circle; thus it is required to inscribe a square in the
circle ABCD.
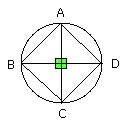 Let two diameters AC, BD of the circle ABCD be drawn at right angles to one
another, and let AB, BC, CD, DA be joined.
Let two diameters AC, BD of the circle ABCD be drawn at right angles to one
another, and let AB, BC, CD, DA be joined.
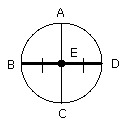 Then, since BE is equal to ED, for E is the centre,
Then, since BE is equal to ED, for E is the centre,
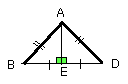 and EA is common and at right angles, therefore the base AB is equal to the
base AD [I. 4].
and EA is common and at right angles, therefore the base AB is equal to the
base AD [I. 4].
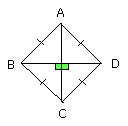 For the same reason each of the straight lines BC, CD is also equal to each of
the straight lines AB, AD; therefore the quadrilateral ABCD is equilateral.
For the same reason each of the straight lines BC, CD is also equal to each of
the straight lines AB, AD; therefore the quadrilateral ABCD is equilateral.
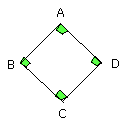 I say next that it is also right-angled.
I say next that it is also right-angled.
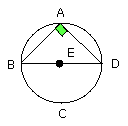 For, since the straight line BD is a diameter of the circle ABCD, therefore
BAD is a semicircle; therefore the angle BAD is right [III. 31].
For, since the straight line BD is a diameter of the circle ABCD, therefore
BAD is a semicircle; therefore the angle BAD is right [III. 31].
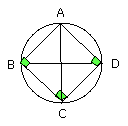 For the same reason each of the angles ABC, BCD, CDA is also right;
For the same reason each of the angles ABC, BCD, CDA is also right;
 therefore the quadrilateral ABCD is right-angled.
therefore the quadrilateral ABCD is right-angled.
 But it was also proved equilateral; therefore it is a square [I. Def. 22]; and
it has been inscribed in the circle ABCD.
But it was also proved equilateral; therefore it is a square [I. Def. 22]; and
it has been inscribed in the circle ABCD.
Therefore in the given circle the square ABCD has been inscribed.
Q.E.F.