About a given circle to circumscribe a square.
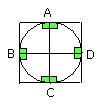
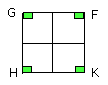
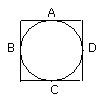 Let ABCD be the given circle; thus it is required to circumscribe a square
about the circle ABCD.
Let ABCD be the given circle; thus it is required to circumscribe a square
about the circle ABCD.
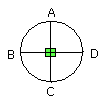 Let two diameters AC, BD of the circle ABCD be drawn at right angles to one
another;
Let two diameters AC, BD of the circle ABCD be drawn at right angles to one
another;
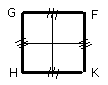
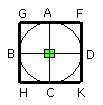 and through the points A, B, C, D let FG, GH, HK, KF be drawn touching the
circle ABCD [III. 16, Por.].
and through the points A, B, C, D let FG, GH, HK, KF be drawn touching the
circle ABCD [III. 16, Por.].
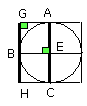
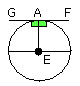 Then, since FG touches the circle ABCD, and EA has been joined from the centre
E to the point of contact at A, therefore the angles at A are right.
Then, since FG touches the circle ABCD, and EA has been joined from the centre
E to the point of contact at A, therefore the angles at A are right.
 For the same reason the angles at the points B, C, D are also right.
For the same reason the angles at the points B, C, D are also right.
 Now, since the angle AEB is right, and the angle EBG is also right, therefore
GH is parallel to AC.
Now, since the angle AEB is right, and the angle EBG is also right, therefore
GH is parallel to AC.
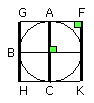 For the same reason AC is parallel to FK, so that GH is also parallel to FK
[I. 30].
For the same reason AC is parallel to FK, so that GH is also parallel to FK
[I. 30].
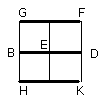 Similarly we can prove that each of the straight lines GF, HK is parallel to
BED.
Similarly we can prove that each of the straight lines GF, HK is parallel to
BED.
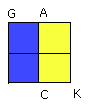 Therefore GK, GC, AK,
Therefore GK, GC, AK,
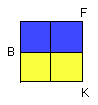 FB, BK are parallelograms
FB, BK are parallelograms
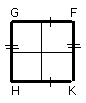 therefore GF is equal to HK, and GH to FK [I. 34].
therefore GF is equal to HK, and GH to FK [I. 34].
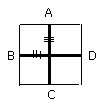 And, since AC is equal to BD,
And, since AC is equal to BD,
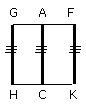 and AC is also equal to each of the straight lines GH, FK,
and AC is also equal to each of the straight lines GH, FK,
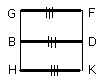 while BD is equal to each of the straight lines GF, HK [I. 34];
while BD is equal to each of the straight lines GF, HK [I. 34];
 therefore the quadrilateral FGHK is equilateral.
therefore the quadrilateral FGHK is equilateral.
 I say next that it is also right-angled.
I say next that it is also right-angled.
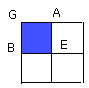 For, since GBEA is a parallelogram,
For, since GBEA is a parallelogram,
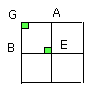 and the angle AEB is right, therefore the angle AGB is also right [I. 34].
and the angle AEB is right, therefore the angle AGB is also right [I. 34].
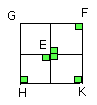 Similarly we can prove that the angles at H, K, F are also right.
Similarly we can prove that the angles at H, K, F are also right.
 Therefore FGHK is right-angled.
Therefore FGHK is right-angled.
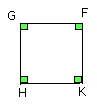
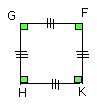 But it was also proved equilateral; therefore it is a square;
But it was also proved equilateral; therefore it is a square;
 and it has been circumscribed about the circle ABCD.
and it has been circumscribed about the circle ABCD.
Therefore about the given circle a square has been circumscribed.
Q.E.F.