To construct an isosceles triangle having each of the angles at the base double of the remaining one.
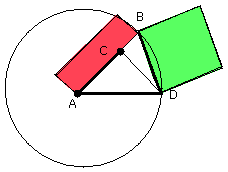
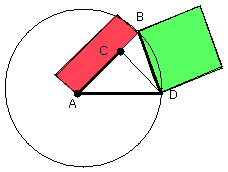
 Let any straight line AB be set out, and let it be cut at the point C so that
the rectangle contained by AB, BC is equal to the square on CA [II. 2];
Let any straight line AB be set out, and let it be cut at the point C so that
the rectangle contained by AB, BC is equal to the square on CA [II. 2];
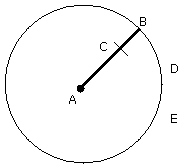 with centre A and distance AB let the circle BDE be described,
with centre A and distance AB let the circle BDE be described,
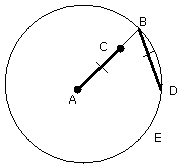 and let there be fitted in the circle BDE the straight line BD equal to the
straight line AC which is not greater than the diameter of the circle BDE
[IV. 1].
and let there be fitted in the circle BDE the straight line BD equal to the
straight line AC which is not greater than the diameter of the circle BDE
[IV. 1].
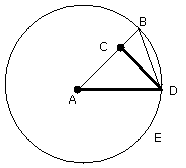 Let AD, DC be joined,
Let AD, DC be joined,
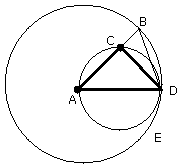 and let the circle ACD be circumscribed about the triangle ACD [IV. 5].
and let the circle ACD be circumscribed about the triangle ACD [IV. 5].
 Then, since the rectangle AB, BC is equal to the square on AC,
Then, since the rectangle AB, BC is equal to the square on AC,
 and AC is equal to BD, therefore the rectangle AB, BC is equal to the square
on BD.
and AC is equal to BD, therefore the rectangle AB, BC is equal to the square
on BD.
 And, since a point B has been taken outside the circle ACD, and from B the two
straight lines BA, BD have fallen on the circle ACD, and one of them cuts it,
while the other falls on it, and the rectangle AB, BC is equal to the square on
BD,
And, since a point B has been taken outside the circle ACD, and from B the two
straight lines BA, BD have fallen on the circle ACD, and one of them cuts it,
while the other falls on it, and the rectangle AB, BC is equal to the square on
BD,
 therefore BD touches the circle ACD [III. 37].
therefore BD touches the circle ACD [III. 37].
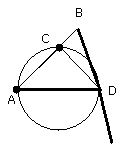 Since, then, BD touches it, and DC is drawn across from the point of contact
at D, therefore the angle BDC is equal to the angle DAC in the alternate
segment of the circle [III. 32].
Since, then, BD touches it, and DC is drawn across from the point of contact
at D, therefore the angle BDC is equal to the angle DAC in the alternate
segment of the circle [III. 32].
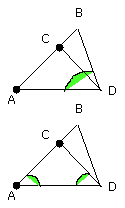 Since, then, the angle BDC is equal to the angle DAC, let the angle CDA be
added to each; therefore the whole angle BDA is equal to the two angles CDA,
DAC.
Since, then, the angle BDC is equal to the angle DAC, let the angle CDA be
added to each; therefore the whole angle BDA is equal to the two angles CDA,
DAC.
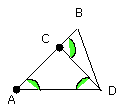 But the exterior angle BCD is equal to the angles CDA, DAC [I. 32];
But the exterior angle BCD is equal to the angles CDA, DAC [I. 32];
 therefore the angle BDA is also equal to the angle BCD.
therefore the angle BDA is also equal to the angle BCD.
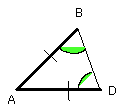 But the angle BDA is equal to the angle CBD, since the side AD is also equal
to AB [I. 5];
But the angle BDA is equal to the angle CBD, since the side AD is also equal
to AB [I. 5];
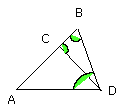 so that the angle DBA is also equal to the angle BCD.
so that the angle DBA is also equal to the angle BCD.
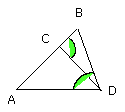
 Therefore the three angles BDA, DBA, BCD are equal to one another.
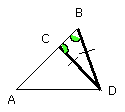
And, since the angle DBC is equal to the angle BCD, the side BD is also equal
to the side DC [I. 6].
Therefore the three angles BDA, DBA, BCD are equal to one another.
And, since the angle DBC is equal to the angle BCD, the side BD is also equal
to the side DC [I. 6].
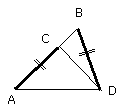 But BD is by hypothesis equal to CA;
But BD is by hypothesis equal to CA;
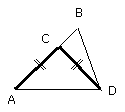 therefore CA is also equal to CD,
therefore CA is also equal to CD,
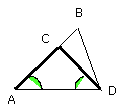 so that the angle CDA is also equal to the angle DAC [I. 5];
so that the angle CDA is also equal to the angle DAC [I. 5];
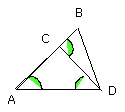 therefore the angles CDA, DAC are double of the angle DAC.
But the angle BCD is equal to the angles CDA, DAC; therefore the angle BCD is
also double of the angle CAD.
therefore the angles CDA, DAC are double of the angle DAC.
But the angle BCD is equal to the angles CDA, DAC; therefore the angle BCD is
also double of the angle CAD.
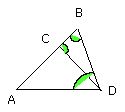 But the angle BCD is equal to each of the angles BDA, DBA; therefore each of
the angles BDA, DBA is also double of the angle DAB.
But the angle BCD is equal to each of the angles BDA, DBA; therefore each of
the angles BDA, DBA is also double of the angle DAB.
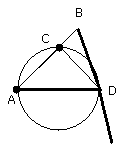
 Therefore the isosceles triangle ABD has been constructed having each of the
angles at the base DB double of the remaining one.
Therefore the isosceles triangle ABD has been constructed having each of the
angles at the base DB double of the remaining one.
Q.E.F.