In a given circle to inscribe an equilateral and equiangular pentagon.
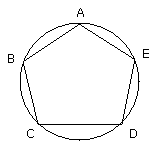 Let ABCDE be the given circle; thus it is required to inscribe in the circle
ABCDE an equilateral and equiangular pentagon.
Let ABCDE be the given circle; thus it is required to inscribe in the circle
ABCDE an equilateral and equiangular pentagon.
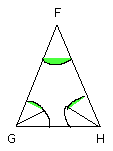 Let the isosceles triangle FGH be set out having each of the angles at G, H
double of the angle at F [IV. 10];
Let the isosceles triangle FGH be set out having each of the angles at G, H
double of the angle at F [IV. 10];
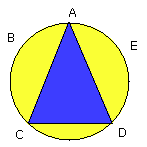 Let there be inscribed in the circle ABCDE the triangle ACD equiangular with
the triangle FGH, so that the angle CAD is equal to the angle at F and the
angles at G, H respectively equal to the angles ACD, CDA [IV. 2];
Let there be inscribed in the circle ABCDE the triangle ACD equiangular with
the triangle FGH, so that the angle CAD is equal to the angle at F and the
angles at G, H respectively equal to the angles ACD, CDA [IV. 2];
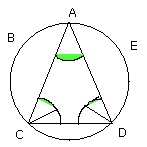 therefore each of the angles ACD, CDA is also double of the angle CAD.
therefore each of the angles ACD, CDA is also double of the angle CAD.
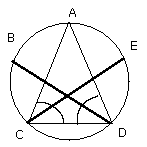 Now let the angles ACD, CDA be bisected respectively by the straight lines CE,
DB [I. 9],
Now let the angles ACD, CDA be bisected respectively by the straight lines CE,
DB [I. 9],
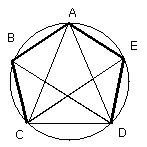 and let AB, BC, DE, EA be joined.
and let AB, BC, DE, EA be joined.
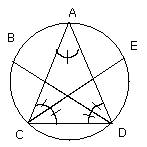 Then, since each of the angles ACD, CDA is double of the angle CAD, and they
have been bisected by the straight lines CE, DB, therefore the five angles
DAC, ACE, ECD, CDB, BDA are equal to one another.
Then, since each of the angles ACD, CDA is double of the angle CAD, and they
have been bisected by the straight lines CE, DB, therefore the five angles
DAC, ACE, ECD, CDB, BDA are equal to one another.
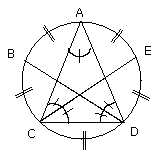 But equal angles stand on equal circumferences [III. 26]; therefore the five
circumferences AB, BC, CD, DE, EA are equal to one another.
But equal angles stand on equal circumferences [III. 26]; therefore the five
circumferences AB, BC, CD, DE, EA are equal to one another.
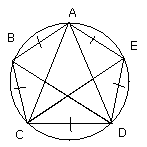 But equal circumferences are subtended by equal straight lines [III. 29];
therefore the five straight lines AB, BC, CD, DE, EA are equal to one another;
But equal circumferences are subtended by equal straight lines [III. 29];
therefore the five straight lines AB, BC, CD, DE, EA are equal to one another;
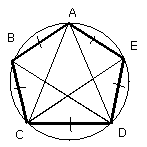 therefore the pentagon ABCDE is equilateral.
therefore the pentagon ABCDE is equilateral.
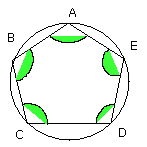 I say next that it is also equiangular.
I say next that it is also equiangular.
 For, since the circumference AB is equal to the circumference DE, let BCD be
added to each;
For, since the circumference AB is equal to the circumference DE, let BCD be
added to each;
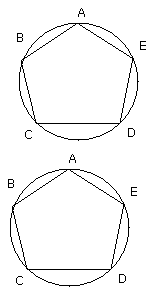 therefore the whole circumference ABCD is equal to the whole circumference EDCB.
therefore the whole circumference ABCD is equal to the whole circumference EDCB.
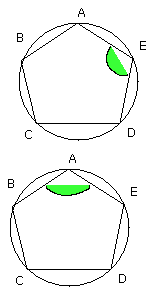 And the angle AED stands on the circumference ABCD, and the angle BAE on the
circumference EDCB; therefore the angle BAE is also equal to the angle
AED [III. 27].
And the angle AED stands on the circumference ABCD, and the angle BAE on the
circumference EDCB; therefore the angle BAE is also equal to the angle
AED [III. 27].
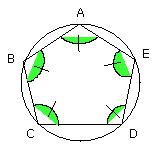 For the same reason each of the angles ABC, BCD, CDE is also equal to each of
the angles BAE, AED; therefore the pentagon ABCDE is equiangular.
For the same reason each of the angles ABC, BCD, CDE is also equal to each of
the angles BAE, AED; therefore the pentagon ABCDE is equiangular.
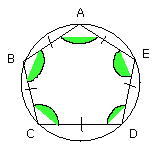 But it was also proved equilateral; therefore in the given circle an
equilateral and equiangular pentagon has been inscribed.
But it was also proved equilateral; therefore in the given circle an
equilateral and equiangular pentagon has been inscribed.
Q.E.F.