In a given pentagon, which is equilateral and equiangular, to inscribe a circle.
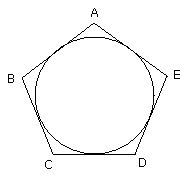 Let ABCDE be the given equilateral and equiangular pentagon; thus it is
required to inscribe a circle in the pentagon ABCDE.
Let ABCDE be the given equilateral and equiangular pentagon; thus it is
required to inscribe a circle in the pentagon ABCDE.
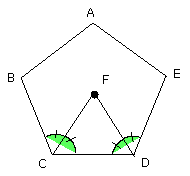 For let the angles BCD, CDE be bisected by the straight lines CF, DF
respectively;
For let the angles BCD, CDE be bisected by the straight lines CF, DF
respectively;
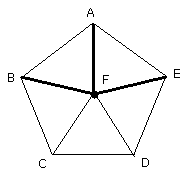 and from the point F, at which the straight lines CF, DF meet one another, let
the straight lines FB, FA, FE be joined.
and from the point F, at which the straight lines CF, DF meet one another, let
the straight lines FB, FA, FE be joined.
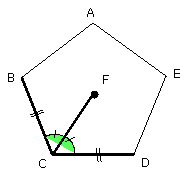 Then, since BC is equal to CD, and CF common, the two sides BC, CF are equal
to the two sides DC, CF; and the angle BCF is equal to the angle DCF;
Then, since BC is equal to CD, and CF common, the two sides BC, CF are equal
to the two sides DC, CF; and the angle BCF is equal to the angle DCF;
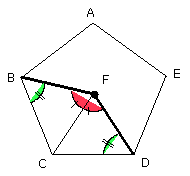 therefore the base BF is equal to the base DF, and the triangle BCF is equal
to the triangle DCF, and the remaining angles will be equal to the remaining
angles, namely those which the equal sides subtend [I. 4].
therefore the base BF is equal to the base DF, and the triangle BCF is equal
to the triangle DCF, and the remaining angles will be equal to the remaining
angles, namely those which the equal sides subtend [I. 4].
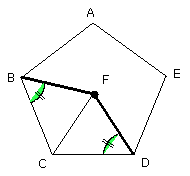 Therefore the angle CBF is equal to the angle CDF.
Therefore the angle CBF is equal to the angle CDF.
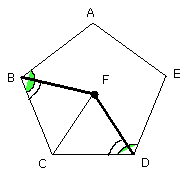 And, since the angle CDE is double of the angle CDF, and the angle CDE is
equal to the angle ABC, while the angle CDF is equal to the angle ABC, while
the angle CDF is equal to the angle CBF;
And, since the angle CDE is double of the angle CDF, and the angle CDE is
equal to the angle ABC, while the angle CDF is equal to the angle ABC, while
the angle CDF is equal to the angle CBF;
 therefore the angle CBA is also double of the angle CDF; therefore the angle
ABF is equal to the angle FBC; therefore the angle ABC has been bisected by
the straight line BF.
therefore the angle CBA is also double of the angle CDF; therefore the angle
ABF is equal to the angle FBC; therefore the angle ABC has been bisected by
the straight line BF.
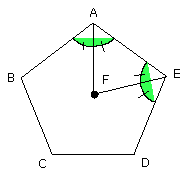 Similarly it can be proved that the angles BAE, AED have also been bisected by
the straight lines FA, FE respectively.
Similarly it can be proved that the angles BAE, AED have also been bisected by
the straight lines FA, FE respectively.
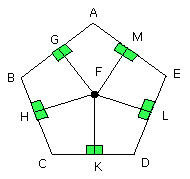 Now let FG, FH, FK, FL, FM be drawn from the point F perpendicular to the
straight lines AB, BC, CD, DE, EA.
Now let FG, FH, FK, FL, FM be drawn from the point F perpendicular to the
straight lines AB, BC, CD, DE, EA.
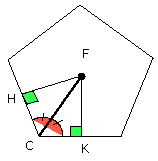 Then, since the angle HCF is equal to the angle KCF, and the right angle FHC
is also equal to the angle FKC, FHC, FKC are two triangles having two angles
equal to two angles and one side equal to one side, namely FC which is common
to them and subtends one of the equal angles;
Then, since the angle HCF is equal to the angle KCF, and the right angle FHC
is also equal to the angle FKC, FHC, FKC are two triangles having two angles
equal to two angles and one side equal to one side, namely FC which is common
to them and subtends one of the equal angles;
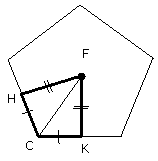 therefore they will also have the remaining sides equal to the remaining sides
[I. 26]; therefore the perpendicular FH is equal to the perpendicular FK.
therefore they will also have the remaining sides equal to the remaining sides
[I. 26]; therefore the perpendicular FH is equal to the perpendicular FK.
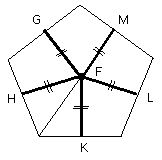 Similarly it can be proved that each of the straight lines FL, FM, FG is also
equal to each of the straight lines FH, FK; therefore the five straight lines
FG, FH, FK, FL, FM are equal to one another.
Similarly it can be proved that each of the straight lines FL, FM, FG is also
equal to each of the straight lines FH, FK; therefore the five straight lines
FG, FH, FK, FL, FM are equal to one another.
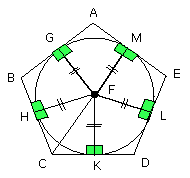 Therefore the circle described with centre F and distance one of the straight
lines FG, FH, FK, FL, FM will pass also through the remaining points; and it
will touch the straight lines AB, BC, CD, DE, EA, because the angles at the
points G, H, K, L, M are right.
Therefore the circle described with centre F and distance one of the straight
lines FG, FH, FK, FL, FM will pass also through the remaining points; and it
will touch the straight lines AB, BC, CD, DE, EA, because the angles at the
points G, H, K, L, M are right.
 For, if it does not touch them, but cuts them, it will result that the
straight line drawn at right angles to the diameter of the circle from its
extremity falls within the circle: which was proved absurd.
For, if it does not touch them, but cuts them, it will result that the
straight line drawn at right angles to the diameter of the circle from its
extremity falls within the circle: which was proved absurd.
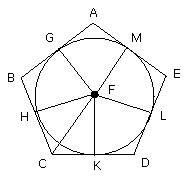 Therefore the circle described with centre F and distance one of the straight
lines FG, FH, FK, FL, FM will not cut the straight lines AB, BC, CD, DE, EA;
therefore it will touch them. Let it be described, as GHKLM.
Therefore the circle described with centre F and distance one of the straight
lines FG, FH, FK, FL, FM will not cut the straight lines AB, BC, CD, DE, EA;
therefore it will touch them. Let it be described, as GHKLM.
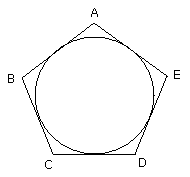 Therefore in the given pentagon, which is equilateral and equiangular, a
circle has been inscribed.
Therefore in the given pentagon, which is equilateral and equiangular, a
circle has been inscribed.
Q.E.F.