About a given pentagon, which is equilateral and equiangular, to circumscribe a circle.
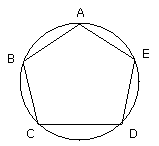 Let ABCDE be the given pentagon, which is equilateral and equiangular; thus it
is required to circumscribe a circle about the pentagon ABCDE.
Let ABCDE be the given pentagon, which is equilateral and equiangular; thus it
is required to circumscribe a circle about the pentagon ABCDE.
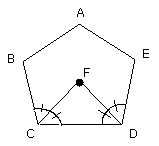 Let the angles BCD, CDE be bisected by the straight lines CF, DF respectively,
Let the angles BCD, CDE be bisected by the straight lines CF, DF respectively,
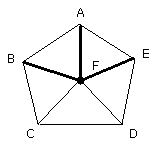 and from the point F, at which the straight lines meet, let the straight lines
FB, FA, FE be joined to the points B, A, E.
and from the point F, at which the straight lines meet, let the straight lines
FB, FA, FE be joined to the points B, A, E.
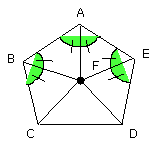 Then in manner similar to the preceding it can be proved that the angles CBA,
BAE, AED have also been bisected by the straight lines FB, FA, FE respectively.
Then in manner similar to the preceding it can be proved that the angles CBA,
BAE, AED have also been bisected by the straight lines FB, FA, FE respectively.
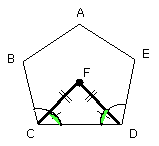 Now, since the angle BCD is equal to the angle CDE, and the angle FCD is half
of the angle BCD, and the angle CDF half of the angle CDE, therefore the angle
FCD is also equal to the angle CDF, so that the side FC is also equal to the
side FD [I. 6].
Now, since the angle BCD is equal to the angle CDE, and the angle FCD is half
of the angle BCD, and the angle CDF half of the angle CDE, therefore the angle
FCD is also equal to the angle CDF, so that the side FC is also equal to the
side FD [I. 6].
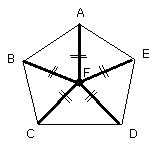 Similarly it can be proved that each of the straight lines FB, FA, FE is also
equal to each of the straight lines FC, FD; therefore the five straight lines
FA, FB, FC, FD, FE are equal to one another.
Similarly it can be proved that each of the straight lines FB, FA, FE is also
equal to each of the straight lines FC, FD; therefore the five straight lines
FA, FB, FC, FD, FE are equal to one another.
Therefore the circle described with centre F and distance one of the straight
lines FA, FB, FC, FD, FE will pass also through the remaining points, and will
have been circumscribed.
Let it be circumscribed, and let it be ABCDE.
Therefore about the given pentagon, which is equilateral and equiangular, a
circle has been circumscribed.
Q.E.F.