In a given circle to inscribe a fifteen-angled figure which shall be both equilateral and equiangular.
 Let ABCD be the given circle; thus it is required to inscribe in the circle
ABCD a fifteen-angled figure which shall be both equilateral and equiangular.
Let ABCD be the given circle; thus it is required to inscribe in the circle
ABCD a fifteen-angled figure which shall be both equilateral and equiangular.
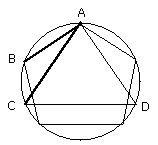 In the circle let there be inscribed a side AC of the equilateral triangle
inscribed in it, and a side AB of an equilateral pentagon;
In the circle let there be inscribed a side AC of the equilateral triangle
inscribed in it, and a side AB of an equilateral pentagon;
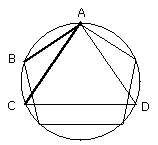 therefore, of equal segments of which there are fifteen in the circle ABCD,
therefore, of equal segments of which there are fifteen in the circle ABCD,
 there will be five in the circumference ABC which is one-third of the circle,
there will be five in the circumference ABC which is one-third of the circle,
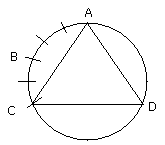
 and there will be three in the circumference AB which is one-fifth of the
circle;
and there will be three in the circumference AB which is one-fifth of the
circle;
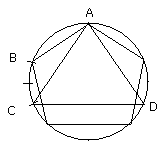 therefore in the remainder BC there will be two of the equal segments.
therefore in the remainder BC there will be two of the equal segments.
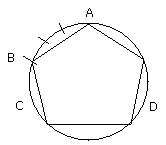
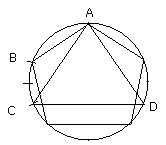 Let BC be bisected at E;
Let BC be bisected at E;
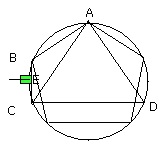 Therefore each of the circumferences BE, EC is a fifteenth of the circle ABCD.
If therefore we join BE, EC and fit into the circle ABCD straight
lines equal to them in contiguity, a fifteen-angled figure which is both
equilateral and equiangular will have been inscribed in it.
Therefore each of the circumferences BE, EC is a fifteenth of the circle ABCD.
If therefore we join BE, EC and fit into the circle ABCD straight
lines equal to them in contiguity, a fifteen-angled figure which is both
equilateral and equiangular will have been inscribed in it.
Q.E.F.
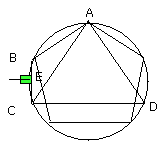 And, in like manner as in the case of the pentagon, if through the points of
division on the circle we draw tangents to the circle, there will be
circumscribed about the circle a fifteen-angled figure which is equilateral
and equiangular.
And, in like manner as in the case of the pentagon, if through the points of
division on the circle we draw tangents to the circle, there will be
circumscribed about the circle a fifteen-angled figure which is equilateral
and equiangular.