If a first magnitude have to a second the same ratio as a third to a fourth, any equimultiples whatever of the first and third will also have the same ratio to any equimultiples whatever of the second and fourth respectively, taken in corresponding order.
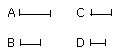For let a first magnitude A have to a second B the same ratio as a third C
to a fourth D;
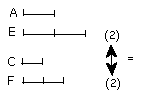and let equimultiples E, F be taken of A, C,
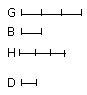and G, H other, chance, equimultiples of B, D;
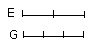I say that, as E is to G,
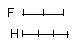so is F to H.
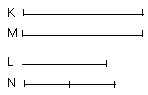
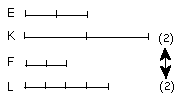For let equimultiples K, L be taken of E, F,
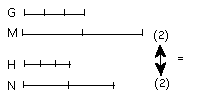and other, chance, equimultiples
M, N of G, H.
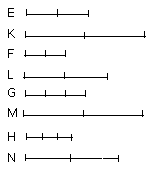
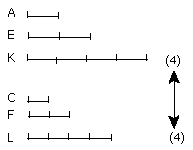Since E is the same multiple of A that F is of C, and equimultiples K, L of
E, F have been taken, therefore K is the same multiple of A that L is of C.
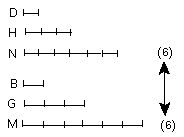For the same reason M is the same multiple of B that N is of D.
And, since, as A is to B, so is C to D, and of A, C equimultiples K, L have
been taken, and of B, D other, chance, equimultiples M, N, therefore, if K is
in excess of M, L also is in excess of N, if it is equal, equal, and if less,
less.
And K, L are equimultiples of E, F, and M, N other, chance, equimultiples of
G, H;
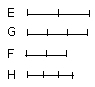therefore, as E is to G, so is F to H.
Therefore etc.
Q.E.D