Equal magnitudes have to the same the same ratio, as also has the same to equal magnitudes.
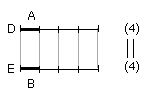
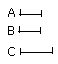Let A, B be equal magnitudes and C any other, chance, magnitude;
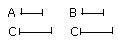I say that each of the magnitudes A, B has the same ratio to C,
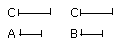and C has the same ratio to each of the magnitudes A, B.
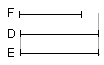
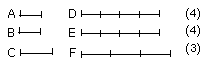For let equimultiples D, E of A, B be taken, and of C another, chance,
multiple F.
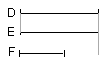
Then, since D is the same multiple of A that E is of B, while A is equal to
B, therefore D is equal to E.
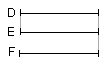
But F is another, chance, magnitude.
If therefore D is in excess of F, E is also in excess of F,
if equal to it, equal;
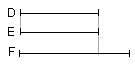and, if less, less.
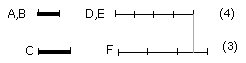And D, E are equimultiples of A, B, while F is another, chance, multiple of
C; therefore, as A is to C, so is B to C.
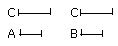I say next that C also has the same ratio to each of the magnitudes A, B.
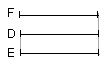
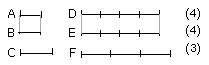For, with the same construction, we can prove similarly that D is equal to
E; and F is some other magnitude.
If therefore F is in excess of D, it is also in excess of E,
if equal, equal;
and, if less, less.
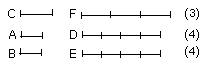And F is a multiple of C, while D, E are other, chance, equimultiples of A, B;
therefore, as C is to A, so is C to B.
Therefore etc.
Porism. From this it is manifest that, if any magnitudes are proportional,
they will also be proportional inversely.
Q.E.D.