Of magnitudes which have a ratio to the same, that which has a greater ratio is greater; and that to which the same has a greater ratio is less.
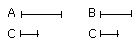For let A have to C a greater ratio than B has to C;
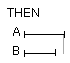I say that A is greater than B.
For, if not, A is either equal to B or less.
Now A is not equal to B;
for in that case each of the magnitudes A, B would have had the same ratio to C;
but they have not; therefore A is not
equal to B.
Nor again is A less than B;
for in that case A would have had to C a less ratio than B has to C;
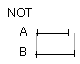but it has not; therefore A is not less than B.
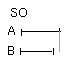But it was proved not to be equal either; therefore A is greater than B.
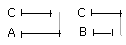Again, let C have to B a greater ratio than C has to A;
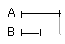I say that B is less than A.
For, if not, it is either equal or greater.
Now B is not equal to A;
for in that case C would have had the same ratio to each of the magnitudes
A, B; but it has not;
therefore A is not equal to B.
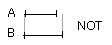Nor again is B greater than A;
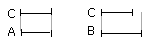for in that case C would have had to B a less ratio than it has to A;
but it has not;
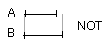therefore B is not greater than A.
But it was proved that it is not equal either; therefore B is less than A.
Therefore etc.
Q.E.D