If two triangles have one angle equal to one angle, the sides about other angles proportional, and the remaining angles either both less or both not less than a right angle, the triangles will be equiangular and will have those angles equal, the sides about which are proportional.
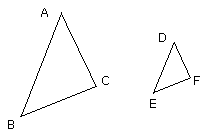
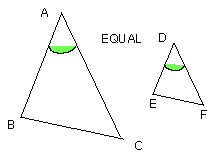 Let ABC, DEF be two triangles having one angle equal to one angle, the angle
BAC to the angle EDF,
Let ABC, DEF be two triangles having one angle equal to one angle, the angle
BAC to the angle EDF,
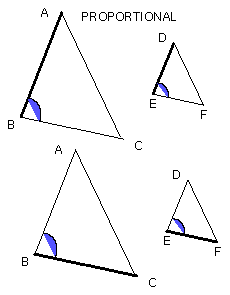 the sides about other angles ABC, DEF
proportional, so that, as AB is to BC, so is DE to EF,
the sides about other angles ABC, DEF
proportional, so that, as AB is to BC, so is DE to EF,
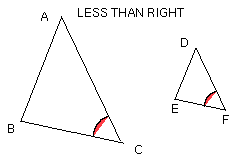 and, first, each of the remaining angles at C, F less than a right angle;
and, first, each of the remaining angles at C, F less than a right angle;
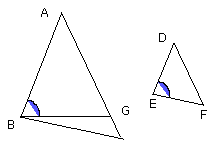 I say that the triangle ABC is equiangular with the triangle DEF, the angle
ABC will be equal to the angle DEF, and the remaining angle, namely the angle
at C, equal to the remaining angle, the angle at F.
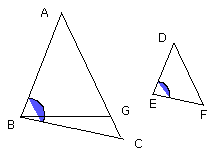
For, if the angle ABC is unequal to the angle DEF, one of them is greater.
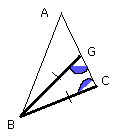
Let the angle ABC be greater; and on the straight line AB, and at the point B
on it, let the angle ABG be constructed equal to the angle DEF.
I say that the triangle ABC is equiangular with the triangle DEF, the angle
ABC will be equal to the angle DEF, and the remaining angle, namely the angle
at C, equal to the remaining angle, the angle at F.
For, if the angle ABC is unequal to the angle DEF, one of them is greater.
Let the angle ABC be greater; and on the straight line AB, and at the point B
on it, let the angle ABG be constructed equal to the angle DEF.
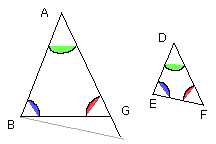 Then, since the angle A is equal to D, and the angle ABG to the angle DEF,
therefore the remaining angle AGB is equal to the remaining angle DFE.
Then, since the angle A is equal to D, and the angle ABG to the angle DEF,
therefore the remaining angle AGB is equal to the remaining angle DFE.
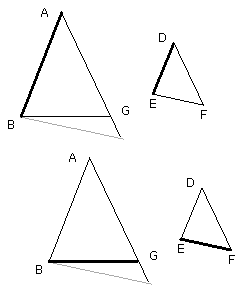 Therefore the triangle ABG is equiangular with the triangle DEF. Therefore,
as AB is to BG, so is DE to EF.
Therefore the triangle ABG is equiangular with the triangle DEF. Therefore,
as AB is to BG, so is DE to EF.
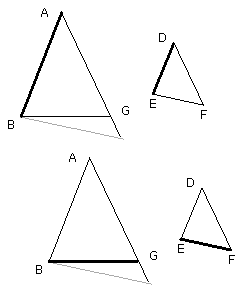 But, as DE is to EF, so by hypothesis is AB to BC; therefore AB has the same
ratio to each of the straight lines BC, BG;
But, as DE is to EF, so by hypothesis is AB to BC; therefore AB has the same
ratio to each of the straight lines BC, BG;
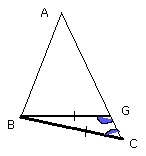 therefore BC is equal to BG, so that the angle at C is also equal to the angle
BGC.
therefore BC is equal to BG, so that the angle at C is also equal to the angle
BGC.
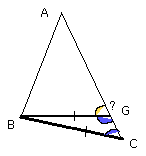 But, by hypothesis, the angle at C is less than a right angle; therefore the
angle BGC is also less than a right angle; so that the angle AGB adjacent to
it is greater than a right angle.
But, by hypothesis, the angle at C is less than a right angle; therefore the
angle BGC is also less than a right angle; so that the angle AGB adjacent to
it is greater than a right angle.
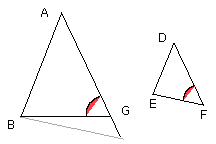 And it was proved equal to the angle at F; therefore the angle at F is also
greater than a right angle.
And it was proved equal to the angle at F; therefore the angle at F is also
greater than a right angle.
 But it is by hypothesis less than a right angle: which is absurd.
Therefore the angle ABC is not unequal to the angle DEF; therefore it is equal
to it.
But it is by hypothesis less than a right angle: which is absurd.
Therefore the angle ABC is not unequal to the angle DEF; therefore it is equal
to it.
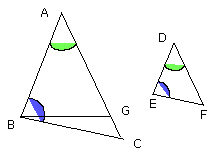 But the angle at A is also equal to the angle at D; therefore the remaining
angle at C is equal to the remaining angle at F.
Therefore the triangle ABC is equiangular with the triangle DEF.
But the angle at A is also equal to the angle at D; therefore the remaining
angle at C is equal to the remaining angle at F.
Therefore the triangle ABC is equiangular with the triangle DEF.
 But, again, let each of the angles at C, F be supposed not less than a right
angle; I say again that, in this case too, the triangle ABC is equiangular
with the triangle DEF.
But, again, let each of the angles at C, F be supposed not less than a right
angle; I say again that, in this case too, the triangle ABC is equiangular
with the triangle DEF.
 For, with the same construction, we can prove similarly that BC is equal to
BG; so that the angle at C is also equal to the angle BGC.
For, with the same construction, we can prove similarly that BC is equal to
BG; so that the angle at C is also equal to the angle BGC.
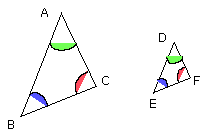 But the angle at C is not less than a right angle; therefore neither is the
angle BGC less than a right angle.
Thus in the triangle BGC the two angles are not less than two right angles:
which is impossible.
Therefore, once more, the angle ABC is not unequal to the angle DEF; therefore
it is equal to it.
But the angle at A is also equal to the angle at D; therefore the remaining
angle at C is equal to the remaining angle at F.
But the angle at C is not less than a right angle; therefore neither is the
angle BGC less than a right angle.
Thus in the triangle BGC the two angles are not less than two right angles:
which is impossible.
Therefore, once more, the angle ABC is not unequal to the angle DEF; therefore
it is equal to it.
But the angle at A is also equal to the angle at D; therefore the remaining
angle at C is equal to the remaining angle at F.
Therefore the triangle ABC is equiangular with the triangle DEF.
Therefore etc.
Q.E.D