To three given straight lines to find a fourth proportional.
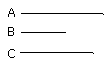 Let A, B, C be the three given straight lines; thus it is required to find a
fourth proportional to A, B, C.
Let A, B, C be the three given straight lines; thus it is required to find a
fourth proportional to A, B, C.
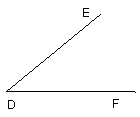 Let two straight lines DE, DF be set out containing any angle EDF;
Let two straight lines DE, DF be set out containing any angle EDF;
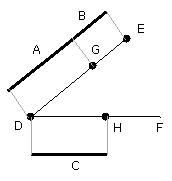 let DG be made equal to A, GE equal to B, and further DH equal to C;
let DG be made equal to A, GE equal to B, and further DH equal to C;
 let GH be joined, and let EF be drawn through E parallel to it.
let GH be joined, and let EF be drawn through E parallel to it.
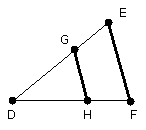
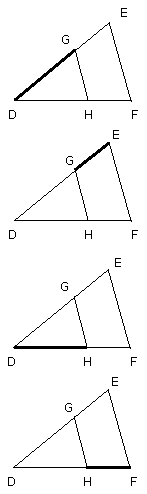 Since, then, GH has been drawn parallel to EF, one of the sides of the
triangle DEF, therefore, as DG is to GE, so is DH to HF.
Since, then, GH has been drawn parallel to EF, one of the sides of the
triangle DEF, therefore, as DG is to GE, so is DH to HF.
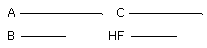 But DG is equal to A, GE to B, and DH to C; therefore, as A is to B, so is C to
HF.
But DG is equal to A, GE to B, and DH to C; therefore, as A is to B, so is C to
HF.
Therefore to the three given straight lines A, B, C a fourth proportional HF has been found.
Q.E.F