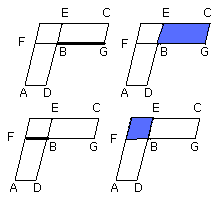
In equal and equiangular parallelograms the sides about the equal angles are reciprocally proportional; and equiangular parallelograms in which the sides about the equal angles are reciprocally proportional are equal.
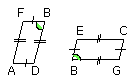 Let AB, BC be equal and equiangular parallelograms having the angles at B equal,
Let AB, BC be equal and equiangular parallelograms having the angles at B equal,
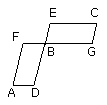 and let DB, BE be placed in a straight line; therefore FB, BG are also in a
straight line.
and let DB, BE be placed in a straight line; therefore FB, BG are also in a
straight line.
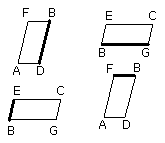 I say that, in AB, BC, the sides about the equal angles are reciprocally
proportionally, that is to say, that, as DB is to BE, so is GB to BF.
I say that, in AB, BC, the sides about the equal angles are reciprocally
proportionally, that is to say, that, as DB is to BE, so is GB to BF.
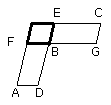 For let the parallelogram FE be completed.
For let the parallelogram FE be completed.
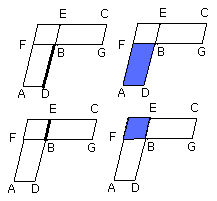
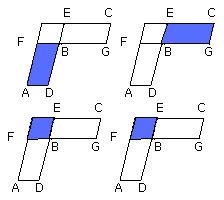 Since, then, the parallelogram AB is equal to the parallelogram BC, and FE is
another area, therefore, as AB is to FE, so is BC to FE.
Since, then, the parallelogram AB is equal to the parallelogram BC, and FE is
another area, therefore, as AB is to FE, so is BC to FE.
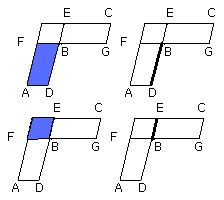 But, as AB is to FE, so is DB to BE,
But, as AB is to FE, so is DB to BE,
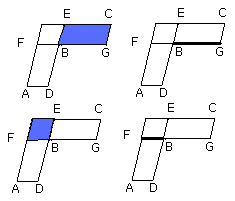 and, as BC is to FE, so is GB to BF.
and, as BC is to FE, so is GB to BF.
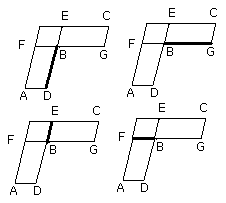 Therefore also, as DB is to BE, so is GB to BF.
Therefore also, as DB is to BE, so is GB to BF.
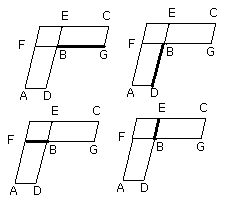 Therefore in the parallelograms AB, BC the sides about the equal angles are
reciprocally proportional.
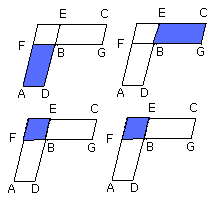
Next, let GB be to BF as DB to BE;
Therefore in the parallelograms AB, BC the sides about the equal angles are
reciprocally proportional.
Next, let GB be to BF as DB to BE;
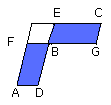 I say that the parallelogram AB is equal to the parallelogram BC.
I say that the parallelogram AB is equal to the parallelogram BC.
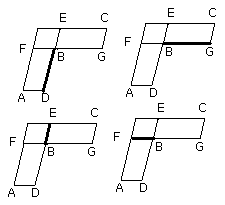 For since, as DB is to BE, so is GB to BF,
For since, as DB is to BE, so is GB to BF,
 while, as DB is to BE, so is the parallelogram AB to the parallelogram FE,
while, as DB is to BE, so is the parallelogram AB to the parallelogram FE,
 and, as GB is to BF, so is the parallelogram BC to the parallelogram FE,
and, as GB is to BF, so is the parallelogram BC to the parallelogram FE,
 therefore also, as AB is to FE, so is BC to FE;
therefore also, as AB is to FE, so is BC to FE;
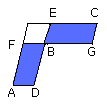 therefore the parallelogram AB is equal to the parallelogram BC.
therefore the parallelogram AB is equal to the parallelogram BC.
Therefore, etc.
Q.E.D.