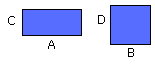
If three straight lines be proportional, the rectangle contained by the extremes is equal to the square on the mean; and, if the rectangle contained by the extremes be equal to the square on the mean, the three straight lines will be proportional.
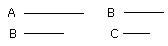Let the three straight lines A, B, C be proportional, so that, as A is to B,
so is B to C;
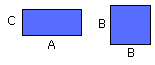I say that the rectangle contained by A, C is equal to the square on B.
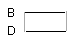Let D be made equal to B.
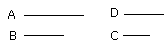Then, since, as A is to B, so is B to C, and B is equal to D, therefore, as A
is to B, so is D to C.
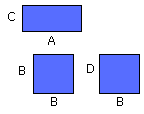
But, if four straight lines be proportional, the rectangle contained by the
extremes is equal to the rectangle contained by the means.
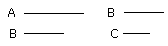so is B to C.
For, with the same construction, since the rectangle A, C is equal to the
square on B, while the square on B is the rectangle B, D, for B is equal to D,
therefore the rectangle A, C is equal to the rectangle B, D.
But, if the rectangle contained by the extremes be equal to that contained by
the means, the four straight lines are proportional.
Therefore, as A is to B, so is D to C.
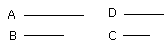But B is equal to D; therefore, as A is to B, so is B to C
Therefore, etc.
Q.E.D.