Similar polygons are divided into similar triangles, and into triangles equal in multitude and in the same ratio as the wholes, and the polygon has to the polygon a ratio duplicate of that which the corresponding side has to the corresponding side.
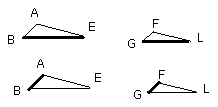
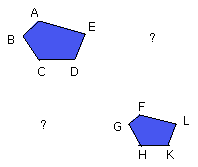
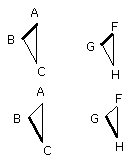
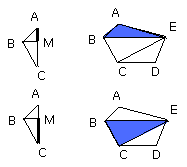
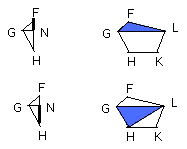
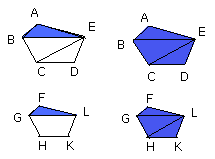
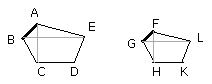 Let ABCDE, FGHKL be similar polygons, and let AB correspond to FG;
Let ABCDE, FGHKL be similar polygons, and let AB correspond to FG;
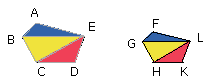 I say that the polygons ABCDE, FGHKL are divided into similar triangles, and
into triangles equal in multitude and in the same ratio as the wholes,
I say that the polygons ABCDE, FGHKL are divided into similar triangles, and
into triangles equal in multitude and in the same ratio as the wholes,
 and the polygon ABCDE has to the polygon FGHKL
and the polygon ABCDE has to the polygon FGHKL
 a ratio duplicate of that which AB has to FG.
a ratio duplicate of that which AB has to FG.
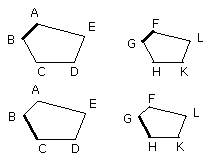
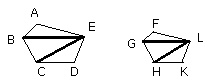 Let BE, EC, GL, LH be joined.
Let BE, EC, GL, LH be joined.
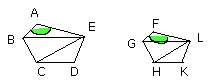 Now, since the polygon ABCDE is similar to the polygon FGHKL, the angle
BAE is equal to the angle GFL;
Now, since the polygon ABCDE is similar to the polygon FGHKL, the angle
BAE is equal to the angle GFL;
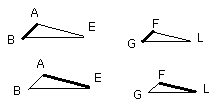 and, as BA is to AE, so is GF to FL.
and, as BA is to AE, so is GF to FL.
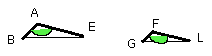 Since then ABE, FGL are two triangles having one angle equal to one angle and
the sides about the equal angles proportional,
Since then ABE, FGL are two triangles having one angle equal to one angle and
the sides about the equal angles proportional,
 therefore the triangle ABE is equiangular with the triangle FGL; so that it
is also similar;
therefore the triangle ABE is equiangular with the triangle FGL; so that it
is also similar;
 therefore the angle ABE is equal to the angle FGL.
therefore the angle ABE is equal to the angle FGL.
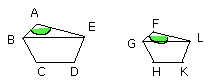 But the whole angle ABC is also equal to the whole angle FGH because of the
similarity of the polygons;
But the whole angle ABC is also equal to the whole angle FGH because of the
similarity of the polygons;
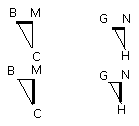
 therefore the remaining angle EBC is equal to the remaining angle LGH.
therefore the remaining angle EBC is equal to the remaining angle LGH.
 And, since, because of the similarity of the triangles ABE, FGL, as EB is to
BA, so is LG to GF,
And, since, because of the similarity of the triangles ABE, FGL, as EB is to
BA, so is LG to GF,
 and moreover also, because of the similarity of the polygons, as AB is to BC,
so is FG to GH,
and moreover also, because of the similarity of the polygons, as AB is to BC,
so is FG to GH,
 therefore, ex equali, as EB is to BC, so is LG to GH;
therefore, ex equali, as EB is to BC, so is LG to GH;
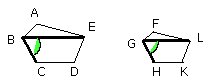 that is, the sides about the equal angles EBC, LGH are proportional;
that is, the sides about the equal angles EBC, LGH are proportional;
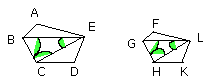 therefore the triangle EBC is equiangular with the triangle LGH.
therefore the triangle EBC is equiangular with the triangle LGH.
 so that the triangle EBC is also similar to the triangle LGH.
For the same reason the triangle ECD is also similar to the triangle LHK.
so that the triangle EBC is also similar to the triangle LGH.
For the same reason the triangle ECD is also similar to the triangle LHK.
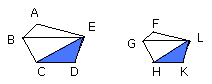
 Therefore the similar polygons ABCDE, FGHKL have been divided into similar
triangles and into tirangles equal in multitude.
Therefore the similar polygons ABCDE, FGHKL have been divided into similar
triangles and into tirangles equal in multitude.
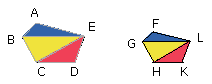
 I say that they are also in the same ratio as the wholes, that is, in such
manner that the triangles are proportional, and ABE, EBC, ECD are antecedents,
while FGL, LGH, LHK are their consequents,
I say that they are also in the same ratio as the wholes, that is, in such
manner that the triangles are proportional, and ABE, EBC, ECD are antecedents,
while FGL, LGH, LHK are their consequents,
 and that the polygon ABCDE has to the polygon FGHKL a ratio duplicate
and that the polygon ABCDE has to the polygon FGHKL a ratio duplicate
 of that which the corresponding side has to the corresponding side, that is AB
to FG.
of that which the corresponding side has to the corresponding side, that is AB
to FG.
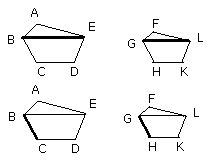
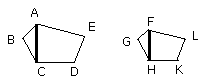 For let AC, FH be joined.
For let AC, FH be joined.
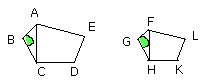 Then since, because of the similarity of the polygons. the angle ABC is equal
to the angle FGH,
Then since, because of the similarity of the polygons. the angle ABC is equal
to the angle FGH,
 and, as AB is to BC, so is FG to GH,
and, as AB is to BC, so is FG to GH,
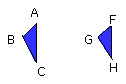 the triangle ABC is equiangular with the triangle FGH;
the triangle ABC is equiangular with the triangle FGH;
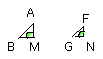 therefore the angle BAC is equal to the angle GFH, and the angle BCA to the
angle GHF.
And, since the angle BAM is equal to the angle GFN, and the angle ABM is also
equal to the angle FGN, therefore the remaining angle AMB is also equal to the
remaining angle FNG;
therefore the angle BAC is equal to the angle GFH, and the angle BCA to the
angle GHF.
And, since the angle BAM is equal to the angle GFN, and the angle ABM is also
equal to the angle FGN, therefore the remaining angle AMB is also equal to the
remaining angle FNG;
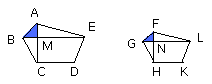 therefore the triangle ABM is equiangular with the triangle FGN.
therefore the triangle ABM is equiangular with the triangle FGN.
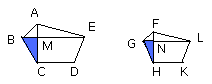 Similarly we can prove that the triangle BMC is also equiangular with the
triangle GNH.
Similarly we can prove that the triangle BMC is also equiangular with the
triangle GNH.
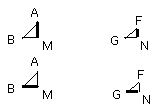 Therefore, proportionally, as AM is to MB, so is FN to NG,
Therefore, proportionally, as AM is to MB, so is FN to NG,
 and, as BM is to MC, so is GN to NH;
and, as BM is to MC, so is GN to NH;
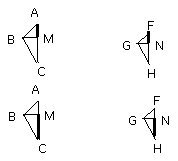 so that, in addition, ex aequali, as AM is to MC, so is FN to NH.
so that, in addition, ex aequali, as AM is to MC, so is FN to NH.
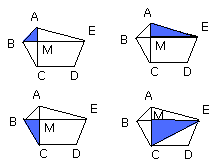 But, as AM is to MC, so is the triangle ABM to MBC, and AME to EMC; for they
are to one another as their bases.
But, as AM is to MC, so is the triangle ABM to MBC, and AME to EMC; for they
are to one another as their bases.
 Therefore also, as one of the antecedents is to one of the consequents, so are
all the antecedents to all the consequents; therefore, as the triangle AMB is
to BMC, so is ABE to CBE.
Therefore also, as one of the antecedents is to one of the consequents, so are
all the antecedents to all the consequents; therefore, as the triangle AMB is
to BMC, so is ABE to CBE.
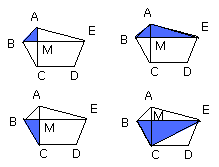
 But, as AMB is to BMC, so is AM to MC; therefore also, as AM is to MC, so is
the triangle ABE to the triangle EBC.
But, as AMB is to BMC, so is AM to MC; therefore also, as AM is to MC, so is
the triangle ABE to the triangle EBC.
 For the same reason also, as FN is to NH, so is the triangle FGL to the
triangle GLH.
For the same reason also, as FN is to NH, so is the triangle FGL to the
triangle GLH.
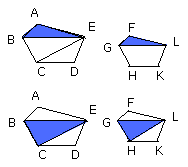 And, as AM is to MC, so is FN to NH; therefore also, as the triangle ABE is
to the triangle BCE, so is the triangle FGL to the triangle GLH;
And, as AM is to MC, so is FN to NH; therefore also, as the triangle ABE is
to the triangle BCE, so is the triangle FGL to the triangle GLH;
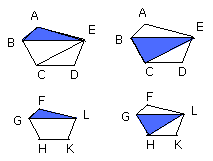 and alternately, as the triangle ABE is to the triangle FGL, so is the
triangle BEC to the triangle GLH.
and alternately, as the triangle ABE is to the triangle FGL, so is the
triangle BEC to the triangle GLH.
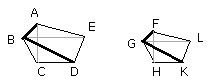 Similarly we can prove, if BD, GK be joined, that,
Similarly we can prove, if BD, GK be joined, that,
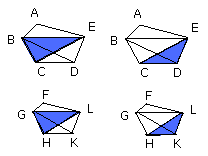 as the triangle BEC is to the triangle LGH, so is the triangle ECD to the
triangle LHK.
as the triangle BEC is to the triangle LGH, so is the triangle ECD to the
triangle LHK.
 And since, as the triangle ABE is to the traingle FGL, so also is EBC to LGH,
and further ECD to LHK, therefore also, as one of the antecedents is to one of
the consequents, so are all of the antecedents to all of the consequents;
therefore, as the triangle ABF is to the triangle FGL, so is the polygon ABCDE
to the polygon FGHKL.
And since, as the triangle ABE is to the traingle FGL, so also is EBC to LGH,
and further ECD to LHK, therefore also, as one of the antecedents is to one of
the consequents, so are all of the antecedents to all of the consequents;
therefore, as the triangle ABF is to the triangle FGL, so is the polygon ABCDE
to the polygon FGHKL.
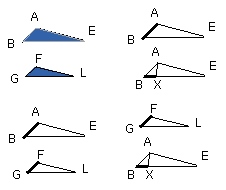 But the triangle ABE has to the triangle FGL a ratio duplicate of that which
the corresponding side AB has to the corresponding side FG; for similar
triangles are in the duplicate ratio of the corresponding sides.
But the triangle ABE has to the triangle FGL a ratio duplicate of that which
the corresponding side AB has to the corresponding side FG; for similar
triangles are in the duplicate ratio of the corresponding sides.
Therefore etc.
Porism. Similarly also it can be proved in the case of quadrilateral that they are in the duplicate ratio of the corresponding sides. And it was also proved in the case of triangles; therefore also, generally, similar rectilineal fugures are to one another in the duplicate ratio of the corresponding sides.
Q.E.D.