Equiangular parallelograms have to one another the ratio compounded of the ratios of their sides.
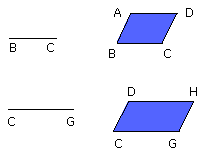
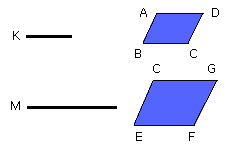
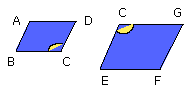Let AC, CF be equiangular parallelograms having the angle BCD equal to the
angle ECG;
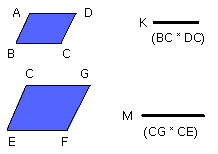I say that the parallelogram AC has to the parallelogram CF the ratio
compounded of the ratios of the sides.
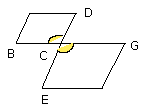For let them be placed so that BC is in a straight line with CG; therefore DC
is also in a straight line with CE.
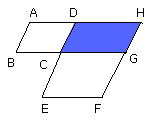Let the parallelogram DG be completed;
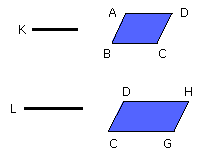
let a straight line K be set out,
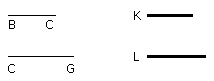and let it be contrived that, as BC is to CG, so is K to L,
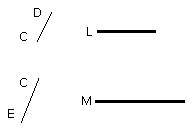and, as DC is to CE, so is L to M.
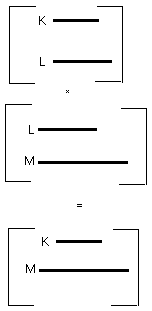Then the ratios of K to L and of L to M are the same as the ratios of the
sides, namely of BC to CG and of DC to CE. But the ratio of K to M is
compounded of the ratio of K to L and of that of L to M;
so that K has also to M the ratio compounded of the ratios of the sides.
Now since, as BC is to CG, so is the parallelogram AC to the parallelogram CH,
while, as BC is to CG, so is K to L, therefore also, as K is to L, so is AC to
CH. [V. 11]
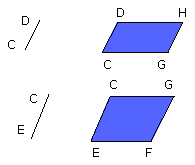Again, since, as DC is to CE, so is the parallelogram CH to CF,
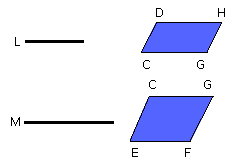while, as DC is to CE, so is L to M, therefore also, as L is to M, so is the
parallelogram CH to the parallelogram CF.
Since then it was proved that, as K is to L, so is the parallelogram AC to the
parallelogram CH, and, as L is to M, so is the parallelogram CH to the
parallelogram CF, therefore, ex aequali, as K is to M, so is AC to the
parallelogram CF.
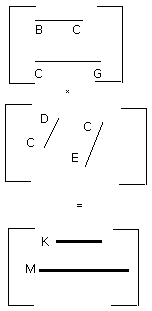
But K has to M the ratio compounded of the ratios of the sides; therefore
AC also has to CF the ratio compounded of the ratios of the sides.
Therefore, etc.
Q.E.D.