Of all the parallelograms applied to the same straight line and deficient by parallelogrammic figures similar and similarly situated to that described on the half of the straight line, that parallelogram is greatest which is applied to the half of the straight line and is similar to the defect.
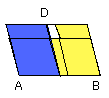
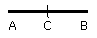 Let AB be a straight line and let it be bisected at C;
Let AB be a straight line and let it be bisected at C;
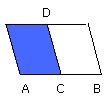 let there be applied to the straight line AB the parallelogram AD deficient by
the parallelogrammic figure DB described on the half of AB, that is, CB;
let there be applied to the straight line AB the parallelogram AD deficient by
the parallelogrammic figure DB described on the half of AB, that is, CB;
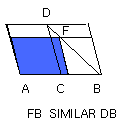 I say that, of all the parallelograms applied to AB and deficient by
parallelogrammic figures similar and similarly situated to DB, AD is greatest.
I say that, of all the parallelograms applied to AB and deficient by
parallelogrammic figures similar and similarly situated to DB, AD is greatest.
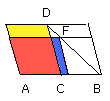 For let there be applied to the straight line AB the parallelogram AF
deficient by the parallelogrammic figure FB similar and similarly situated to
DB;
For let there be applied to the straight line AB the parallelogram AF
deficient by the parallelogrammic figure FB similar and similarly situated to
DB;
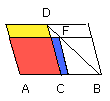 I say that AD is greater than AF.
I say that AD is greater than AF.
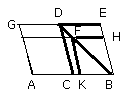 For, since the parallelogram DB is similar to the parallelogram FB, they are
about the same diameter.
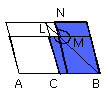
Let their diameter DB be drawn, and let the figure be described.
For, since the parallelogram DB is similar to the parallelogram FB, they are
about the same diameter.
Let their diameter DB be drawn, and let the figure be described.
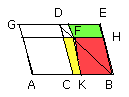 Then, since CF is equal to FE, [I. 43] and FB is common, therefore the whole
CH is equal to the whole KE.
Then, since CF is equal to FE, [I. 43] and FB is common, therefore the whole
CH is equal to the whole KE.
 But CH is equal to CG, since AC is also equal to CB.
But CH is equal to CG, since AC is also equal to CB.
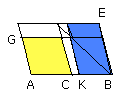 Therefore GC is also equal to EK.
Therefore GC is also equal to EK.
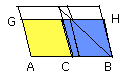
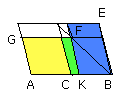 Let CF be added to each;
Let CF be added to each;
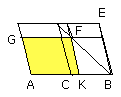 therefore the whole AF
therefore the whole AF
 is equal to the gnomon LMN;
is equal to the gnomon LMN;
 so that the parallelogram DB, that is, AD, is greater than the parallelogram AF.
so that the parallelogram DB, that is, AD, is greater than the parallelogram AF.
Therefore etc.
Q.E.D.