To a given straight line to apply a parallelogram equal to a given rectilineal figure and deficient by a parallelogrammic figure similar to a given one: thus the given rectilineal figure must not be greater than the parallelogram described on the half of the straight line and similar to the defect.
Let AB be the given straight line,
C the given rectilineal figure to which the figure to be applied to AB is
required to be equal,
not being greater than the parallelogram described on the half of AB and
similar to the defect,
and D the parallelogram to which the defect is required to be similar;
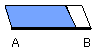thus it is required to apply to the given straight line AB a parallelogram
equal to the given rectilineal figure C and deficient by a parallelogrammic
figure which is similar to D.
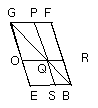
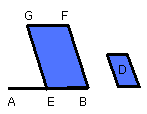Let AB be bisected at the point E, and on EB let EBFG be described similar and
similarly situated to D;
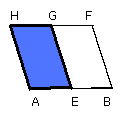let the parallelogram AG be completed.
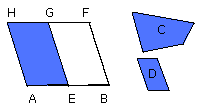If then AG is equal to C, that which was enjoined will have been done; for
there has been applied to the given straight line AB the parallelogram AG
equal to the given rectilineal figure C and deficient by a parallelogrammic
figure GB which is similar to D.
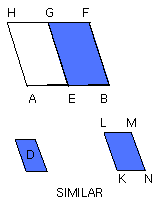
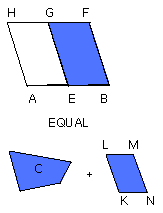But, if not, let HE be greater than C. Now HE is equal to GB; therefore GB is
also greater than C. Let KLMN be constructed at once equal to the excess by
which GB is greater than C and similar and similarly situated to D.
But D is similar to GB; therefore KM is also similar to GB.
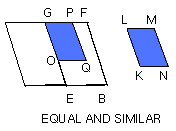Let, then, KL correspond to GE, and LM to GF. Now, since GB is equal to C,
KM, therefore GB is greater than KM; therefore also GE is greater than KL, and
GF than LM.
Let GO be made equal to KL, and GP equal to LM; and let the parallelogram OGPQ
be completed; therefore it is equal and similar to KM.
Therefore GQ is also similar to GB; therefore GQ is about the same diameter
with GB.
Let GQB be their diameter, and let the figure be described.
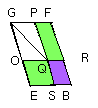
Then, since BQ is equal to C, KM, and in them GQ is equal to KM,
therefore the remainder, the gnomon UWV, is equal to the remainder C.
And, since PR is equal to OS, let QB be added to each; therefore the whole PB
is equal to the whole OB.
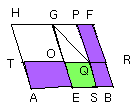But OB is equal to TE, since the side AE is also equal to the side EB;
therefore TE is also equal to PB.
Let OS be added to each; therefore the whole TS is equal to the whole, the
gnomon VWU.
But the gnomon VWU was proved equal to C; therefore TS is also equal to C.
Therefore to the given straight line AB there has been applied the parallelogram ST equal to the given rectilineal figure C and deficient by a parallelogrammic figure QB which is similar to D.
Q.E.F.