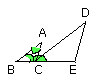
If two triangles having two sides proportional to two sides be placed together at one angle so that their corresponding sides are also parallel, the remaining sides of the triangles will be in a straight line.
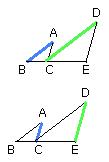Let ABC, DCE be two triangles having the two sides BA, AC proportional to the
two sides DC, DE, so that, as AB is to AC, so is DC to DE, and AB parallel to
DC, and AC to DE;
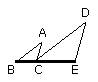I say that BC is in a straight line with CE.
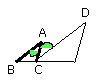For, since AB is parallel to DC, and the straight line AC has fallen upon
them, the alternate angles BAC, ACD are equal to one another.
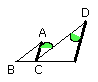For the same reason the angle CDE is also equal to the angle ACD;
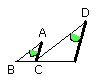so that the angle BAC is equal to the angle CDE.
And, since ABC, DCE are two triangles having one angle, the angle at A, equal
to one angle, the angle at D, and the sides about the equal angles
proportional, so that, as BA is to AC, so is CD to DE,
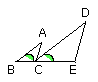therefore the triangle ABC is equiangular with the triangle DCE;
therefore the angle ABC is equal to the angle DCE.
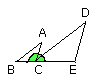
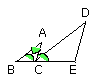But the angle ACD was also proved equal to the angle BAC; therefore the whole
angle ACE is equal to the two angles ABC, BAC.
Let the angle ACB be added to each; therefore the angles ACE, ACB are equal to
the angles BAC, ACB, CBA.
But the angles BAC, ABC, ACB are equal to two right angles; therefore the
angles ACE, ACB are also equal to two right angles.
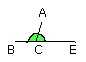Therefore with a straight line AC, and at the point C on it, the two straight
lines BC, CE not lying on the same side make the adjacent angles ACE, ACB
equal to two right angles; therefore BC is in a straight line with CE. [I. 14]
Therefore, etc.
Q.E.D.